题目内容
已知M、N分别在正方形ABCD的边DA、AB上,且AM=AN,过A作BM的垂线,垂足为P,求证:∠APN=∠BNC.
 证明:延长AP交DC于E,连接NE,
证明:延长AP交DC于E,连接NE,∵AP⊥BM,
∴∠APB=∠BPE=∠APM=90°,
∵正方形ABCD,
∴AB∥CD,AB=CD,∠ABC=∠DCB=90°,
∴∠BPE+∠BCD=180°,
∴P、B、C、E四点共圆,
而∠PAM+∠AMP=90°,∠AMP+∠ABM=90°,
∴∠ABM=∠PAM=∠EAD,
∴△ABM≌△DAE,
∴DE=AM=AN,
∴CE=BN,
∴四边形NBCE是矩形,
∴N、B、C、E四点共圆,
即N、B、C、E、P五点共圆,
∴∠NPB=∠NCB,
∵∠APN+∠BPN=90°,∠BCN+∠BNC=90°,
∴∠APN=∠BNC.
分析:延长AP交DC于E,连接NE,由∠BPE+∠BCD=180°,证出P、B、C、E四点共圆,由△ABM和△DAE全等,推出CE=BN,得出矩形BNEC,证出N、B、C、E四点共圆,即N、B、C、E、P五点共圆,即可得出答案.
点评:本题主要考查了矩形的性质和判定,正方形的性质和判定,全等三角形的性质和判定,确定圆的条件等知识点,解此题的关键是证明∠NPB和∠NCB相等.题目较好但有一定的难度.

练习册系列答案
相关题目

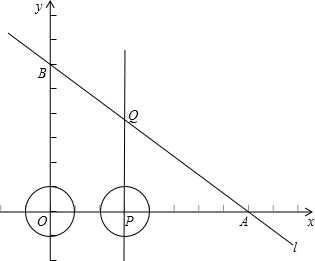 轴分别交于点A、B.
轴分别交于点A、B.