��Ŀ����
��2013•���ݣ���ƽ��ֱ������ϵ�У���֪M1��3��2����N1��5��-1�����߶�M1N1ƽ�����߶�MN����ע��M1��M��N1��N�ֱ�Ϊ��Ӧ�㣩��
��1����M��-2��5������ֱ��д��N�����꣮
��2���ڣ�1���ʵ������£���N��������y=
x2+
x+k�ϣ���������߶�Ӧ�ĺ�������ʽ��
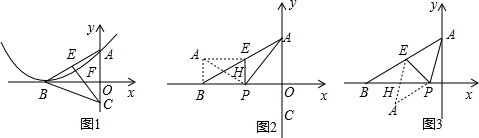
��3���ڣ�2���������£��������߶���ΪB����y�ύ�ڵ�A����EΪ�߶�AB�е㣬��C��0��m����y�Ḻ������һ���㣬�߶�EC���߶�BO�ཻ��F����OC��OF=2��
����m��ֵ��
��4���ڣ�3���������£�����P��B���������x�������������˶�����P�˶���ʲôλ��ʱ����BP��Ϊ���٣�������ABP�ر�PE�۵�����APE���PBE�ص����ֵ����ǡ��Ϊ��ʱ�ġ�ABP�����
�����ʱBP�ij��ȣ�

��1����M��-2��5������ֱ��д��N�����꣮
��2���ڣ�1���ʵ������£���N��������y=
| 1 |
| 6 |
2
| ||
| 3 |
��3���ڣ�2���������£��������߶���ΪB����y�ύ�ڵ�A����EΪ�߶�AB�е㣬��C��0��m����y�Ḻ������һ���㣬�߶�EC���߶�BO�ཻ��F����OC��OF=2��
| 3 |
��4���ڣ�3���������£�����P��B���������x�������������˶�����P�˶���ʲôλ��ʱ����BP��Ϊ���٣�������ABP�ر�PE�۵�����APE���PBE�ص����ֵ����ǡ��Ϊ��ʱ�ġ�ABP�����
| 1 |
| 4 |

��������1�����ȸ��ݵ�M���ƶ�����͵�λ�õ���N��ƽ�Ʒ���͵�λ��Ȼ����ƽ�Ʒ���͵�λ�����ƶ����ɣ�
��2������N��������뺯���Ľ���ʽ�������kֵ��
��3���䷽��ȷ����B��A��E�����꣬����CO��OF=2��
��m��ʾ���߶�CO��FO��BF�ij�������S��BEC=S��EBF+S��BFC=
S��ABC�õ��й�m�ķ������m��ֵ���ɣ�
��4���ֵ���BPE����APEʱ������BPE=��APEʱ������BPE����APEʱ��������������ۼ��ɣ�
��2������N��������뺯���Ľ���ʽ�������kֵ��
��3���䷽��ȷ����B��A��E�����꣬����CO��OF=2��
| 3 |
| 1 |
| 2 |
��4���ֵ���BPE����APEʱ������BPE=��APEʱ������BPE����APEʱ��������������ۼ��ɣ�
����⣺��1������ͼ��ƽ�ƹ����У���Ӧ���ƽ�ƹ�����ͬ��
�ɵ�M����M���֪����ĺ������5���������3��
�ʵ�N�������Ϊ��5-5��-1+3��������0��2����
N��0��2����
��2����N��0��2����������y=
x2+
x+k��
��k=2
�������ߵĽ���ʽΪy=
x2+
x+2
��3����y=
x2+
x+2=
��x+2
��2
��B��-2
��0����A��0��2����E��-
��1��
��CO��OF=2��
��CO=-m��FO=-
m��BF=2
+
m
��S��BEC=S��EBF+S��BFC=
S��ABC
��
��2
+
m����-m+1��=
��
��2
(2-m)
�����ã�m2+m=0
��m=-1��0
��m��0
��m=-1
��4����Rt��ABO��tan��ABO=
=
=
���ABO=30�㣬AB=2AO=4
�ٵ���BPE����APEʱ������A1B����ۺ���ͼ2��A1Ϊ���ۺ�A������㣬��EHP���ص����֣�
��EΪAB�е㣬��S��AEP=S��BEP=
S��ABP
��S��EHP=
S��ABP
��S��A1HE=S��EHP=S��BHP=
S��ABP
��A1H=HP��EH=HB=1
���ı���A1BPEΪƽ���ı���
��BP=A1E=AE=2
��BP=2
�ڵ���BPE=��APEʱ���ص��������Ϊ��ABP�����һ�룬���������⣻
�۵���BPE����APEʱ��
����ۺ���ͼ3��A1Ϊ���ۺ�A������㣮��EHP���ص�����
��EΪAB�е㣬
��S��AEP=S��BEP=
S��ABP
��S��EHP=
S��ABP��S��EBH=S��EHP=S��A1HP=
S��ABP
��BH=HP��EH=HA1=1
�֡�BE=EA=2
��EH
AP��
��AP=2
�ڡ�APB�У���ABP=30�㣬AB=4��AP=2��
���APB=90�㣬
��BP=2
��
�ۺϢ٢ڢ�֪��BP=2��2
��
�ɵ�M����M���֪����ĺ������5���������3��
�ʵ�N�������Ϊ��5-5��-1+3��������0��2����
N��0��2����

��2����N��0��2����������y=
| 1 |
| 6 |
| 2 |
| 3 |
| 3 |
��k=2
�������ߵĽ���ʽΪy=
| 1 |
| 6 |
| 2 |
| 3 |
| 3 |
��3����y=
| 1 |
| 6 |
| 2 |
| 3 |
| 3 |
| 1 |
| 6 |
| 3 |
��B��-2
| 3 |
| 3 |
��CO��OF=2��
| 3 |
��CO=-m��FO=-
| ||
| 2 |
| 3 |
| ||
| 2 |
��S��BEC=S��EBF+S��BFC=
| 1 |
| 2 |
��
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
�����ã�m2+m=0
��m=-1��0
��m��0
��m=-1
��4����Rt��ABO��tan��ABO=
| AO |
| BO |
| 2 | ||
2
|
| ||
| 3 |
���ABO=30�㣬AB=2AO=4
�ٵ���BPE����APEʱ������A1B����ۺ���ͼ2��A1Ϊ���ۺ�A������㣬��EHP���ص����֣�
��EΪAB�е㣬��S��AEP=S��BEP=
| 1 |
| 2 |
��S��EHP=
| 1 |
| 4 |
��S��A1HE=S��EHP=S��BHP=
| 1 |
| 4 |
��A1H=HP��EH=HB=1
���ı���A1BPEΪƽ���ı���
��BP=A1E=AE=2
��BP=2
�ڵ���BPE=��APEʱ���ص��������Ϊ��ABP�����һ�룬���������⣻
�۵���BPE����APEʱ��
����ۺ���ͼ3��A1Ϊ���ۺ�A������㣮��EHP���ص�����
��EΪAB�е㣬
��S��AEP=S��BEP=
| 1 |
| 2 |
��S��EHP=
| 1 |
| 4 |
| 1 |
| 4 |
��BH=HP��EH=HA1=1
�֡�BE=EA=2
��EH
| �� |
. |
| 1 |
| 2 |
��AP=2
�ڡ�APB�У���ABP=30�㣬AB=4��AP=2��
���APB=90�㣬
��BP=2
| 3 |
�ۺϢ٢ڢ�֪��BP=2��2
| 3 |
������������Ҫ�����˵��ƽ�ơ����κ�������ʽ��ȷ����ͼ���۵����⼰ͼ���������Ҫ֪ʶ�㣬ͬʱ�������˷������۵���ѧ˼�룬�ѶȽϴ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��2013•���ݣ�һ�����ձ���װ��һ��С�ձ�����С�ձ��з���һ�����ӣ������dz���Ŀ���СԲ������С�ձ���עˮ��ˮ�����ٶȺ㶨���䣬С�ձ���ע����ˮ��������ձ��У�����ʼ�ձ��������������м䣮��x��ʾעˮʱ�䣬��y��ʾ���ӵĸ߶ȣ���������ʾy��x֮���ϵ��ѡ���ǣ�������
��2013•���ݣ�һ�����ձ���װ��һ��С�ձ�����С�ձ��з���һ�����ӣ������dz���Ŀ���СԲ������С�ձ���עˮ��ˮ�����ٶȺ㶨���䣬С�ձ���ע����ˮ��������ձ��У�����ʼ�ձ��������������м䣮��x��ʾעˮʱ�䣬��y��ʾ���ӵĸ߶ȣ���������ʾy��x֮���ϵ��ѡ���ǣ������� ��2013•���ݣ���ͼ����ֱ֪��a��b����a��b֮��ľ���Ϊ4����A��ֱ��a�ľ���Ϊ2����B��ֱ��b�ľ���Ϊ3��AB=
��2013•���ݣ���ͼ����ֱ֪��a��b����a��b֮��ľ���Ϊ4����A��ֱ��a�ľ���Ϊ2����B��ֱ��b�ľ���Ϊ3��AB= ��2013•���ݣ��������Ҵ���治�����ճ�Ⱥ��ͬʱ����һ����ѧ�ҡ������ң���������ƹ�һ��Բ����ͼ��ʾ�����������ഹֱ�Ļ��ۣ����ۿ��Ⱥ��Բ��ƣ���һ��û�е��Ե�ľ��������A��B���ڻ��������ɻ��������ʲ���λ��ľ���е�P����С���У�����ľ���Ļ����Ϳ��Ի���һ��Բ������AB=20cm������Բ�İ뾶Ϊ
��2013•���ݣ��������Ҵ���治�����ճ�Ⱥ��ͬʱ����һ����ѧ�ҡ������ң���������ƹ�һ��Բ����ͼ��ʾ�����������ഹֱ�Ļ��ۣ����ۿ��Ⱥ��Բ��ƣ���һ��û�е��Ե�ľ��������A��B���ڻ��������ɻ��������ʲ���λ��ľ���е�P����С���У�����ľ���Ļ����Ϳ��Ի���һ��Բ������AB=20cm������Բ�İ뾶Ϊ ��2013•���ݣ�С����С����һ������¥ǰ�п�¥����ߣ�С��˵������¥����20�㣡��С��ȴ����ΪȻ����20�㣿�ҿ�û�У�������֪���ˣ���С��˵�����б��£��㲻����Ҳ�����ף���С��������˵����û���⣡����������һ���ɣ���С����С����¥�������ѡA��B���㣬����������ͼ�����о���CDEF��ʾ¥�壬AB=150�ף�CD=10�ף���A=30�㣬��B=45�㣬��A��C��D��B�ĵ���ͬһֱ���ϣ��ʣ�
��2013•���ݣ�С����С����һ������¥ǰ�п�¥����ߣ�С��˵������¥����20�㣡��С��ȴ����ΪȻ����20�㣿�ҿ�û�У�������֪���ˣ���С��˵�����б��£��㲻����Ҳ�����ף���С��������˵����û���⣡����������һ���ɣ���С����С����¥�������ѡA��B���㣬����������ͼ�����о���CDEF��ʾ¥�壬AB=150�ף�CD=10�ף���A=30�㣬��B=45�㣬��A��C��D��B�ĵ���ͬһֱ���ϣ��ʣ�