题目内容
【题目】已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．
（1）如图①，当直线l与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；
（2）如图②，当直线l与⊙O相交于点E，F时，若∠DAE=18°，求∠BAF的大小．
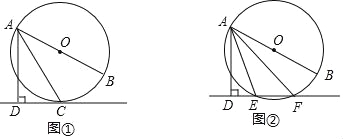
【答案】(1) 30°，（2）18°，
【解析】
试题分析：（1）连接OD，易证OC∥AD，所以∠OCA=∠DAC，由因为OA=OC，所以∠OAC=∠OCA；
（2）连接BE，AB是⊙O的直径，所以∠AEB=90°，从而可知∠BEF=∠DAE=18°，由圆周角定理可知：∠BAF=∠BEF=18°
试题解析：（1）连接OC、
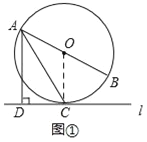
∵l是⊙O的切线，
∴OC⊥l，
∵AD⊥l，
∴OC∥AD，
∴∠OCA=∠DAC=30°，
∵OA=OC，
∴∠OAC=∠OCA=30°，
（2）连接BE，
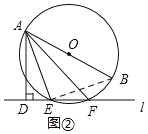
∵AB是⊙O的直径，
∴∠AEB=90°，
∴∠AED+∠BEF=90°，
∵∠AED+∠DAE=90°，
∴∠BEF=∠DAE=18°，
∵
，
∴∠BAF=∠BEF=18°
练习册系列答案
应用题作业本系列答案
相关题目
【题目】根据国家发改委实施“阶梯电价”的有关文件要求，某市结合地方实际，决定对居民生活用电实行“阶梯电价”收费，具体收费标准见表：
一户居民一个月用电量的范围 | 电费价格（单位：元/度） |
不超过200度 | a |
超过200度的部分 | b |
已知4月份，该市居民甲用电250度，交电费130元；居民乙用电400度，交电费220元．
（1）求出表中a和b的值；
（2）实行“阶梯电价”收费以后，该市一户居民月用电多少度时，其当月的平均电价每度不超过0.56元？
