题目内容
如图，已知∠ABD=∠C=90°，AD=12，AC=BD，∠BAD=30°，则BC= ．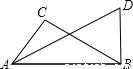
【答案】分析：首先由直角三角形ABD中，∠BAD=30°，得BD=
AD=6，则由已知得AC=BD=6，再由勾股定理求出AB，然后由直角三角形ACB运用勾股定理求出BC．
解答：解：已知∠ABD=∠C=90°，AD=12，AC=BD，∠BAD=30°，
∴BD=
AD=
×12=6，
∴AC=BD=6，
在直角三角形ABD中，根据勾股定理得：
AB=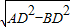
=
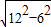=6
，
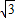在直角三角形ACB中，根据勾股定理得：
BC=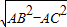
=
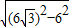=6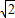
．
故答案为：6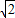
．
点评：此题考查的知识点是解直角三角形，关键是运用直角三角形中30°的性质和勾股定理求解．
AD=6，则由已知得AC=BD=6，再由勾股定理求出AB，然后由直角三角形ACB运用勾股定理求出BC．解答：解：已知∠ABD=∠C=90°，AD=12，AC=BD，∠BAD=30°，
∴BD=
AD=×12=6，∴AC=BD=6，
在直角三角形ABD中，根据勾股定理得：
AB=
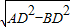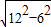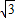==6，在直角三角形ACB中，根据勾股定理得：
BC=
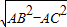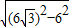==6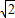．故答案为：6
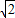．点评：此题考查的知识点是解直角三角形，关键是运用直角三角形中30°的性质和勾股定理求解．
练习册系列答案
相关题目
17、如图，已知∠ABD=∠BDA=∠ADC=∠DCA=75度．请你写出由已知条件能够推出的四个有关线段关系的正确结论（注意：不添加任何字母和辅助线，线段关系仅限于垂直、相等）
（2012•江门模拟）如图，已知△ABD和△ACE都是等边三角形，CD、BE相交于点F．
如图，已知△ABD沿BD平移到了△FCE的位置，BE=10，CD=4，则平移的距离是
如图，已知∠ABD=∠ACD=90°，∠CBD=∠BCD，求证：AD平分∠BAC．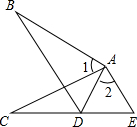
如图，已知△ABD和△ACE，AD=AE，∠1=∠2，要判定△ABD≌△ACE，还需要添加一个条件，这个条件可以是