题目内容
如图，已知△ABC中，AD⊥BC于点D，AE为∠BAC的平分线，且∠B=36°，∠C=66°．求∠DAE的度数．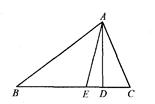
16°
试题分析：先根据三角形的内角和定理求得∠BAC的度数，再根据角平分线的性质求得∠CAE的度数，由垂直的性质可得∠ABD=90°，再根据三角形的内角和定理求得∠CAD度数，从而可以求得结果.
∵∠B=36°，∠C=66°
∴∠BAC=180°-∠ABC-∠ABC=180°-36°-68°=76°
∵AE为∠BAC的平分线
∴∠CAE=
∠BAC==38°∵AD⊥BC于D
∴∠ABD=90°
∴∠CAD=180°-∠C-∠ABD=180°-68°-90°=22°
∴∠DAE=∠CAE-∠CAD=38°-22°=16°.
点评：解题的关键是熟练掌握角的平分线把角分成相等的两个小角，且都等于大角的一半.
练习册系列答案
相关题目
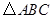中，∠C=90°，∠ABC=45°，AB=6，点D在AB边上，点E在BC边上（不与点B、C重合），且DA=DE，则AD的取值范围是 ． 
