题目内容
 已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.
已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.(1)则AB中点M对应的数是
40
40
;(M点使AM=BM)(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动;
①PQ多少秒以后相遇?
②设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是多少吗?
分析:(1)直接根据中点坐标公式求出M点对应的数;
(2)①先求出AB的长,再设t秒后P、Q相遇即可得出关于t的一元一次方程,求出t的值即可;
②由①中t的值可求出P、Q相遇时点P移动的距离,进而可得出C点对应的数.
(2)①先求出AB的长,再设t秒后P、Q相遇即可得出关于t的一元一次方程,求出t的值即可;
②由①中t的值可求出P、Q相遇时点P移动的距离,进而可得出C点对应的数.
解答:解:(1)∵A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100,
∴
=60;
则AB中点M对应的数是100-60=40;
故答案为:40.
(2)①∵A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100,
∴AB=100+20=120,
设t秒后P、Q相遇,
∵电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,
∴6t+4t=120,解得t=12秒;
答:PQ经过12秒以后相遇;
②∵由①可知,经过12秒P、Q相遇,
∴此时点P走过的路程=6×12=72单位,
∴此时C点表示的数为100-72=28.
答:C点对应的数是28.
∴
| 100-(-20) |
| 2 |
则AB中点M对应的数是100-60=40;
故答案为:40.
(2)①∵A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100,
∴AB=100+20=120,
设t秒后P、Q相遇,
∵电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,
∴6t+4t=120,解得t=12秒;
答:PQ经过12秒以后相遇;
②∵由①可知,经过12秒P、Q相遇,
∴此时点P走过的路程=6×12=72单位,
∴此时C点表示的数为100-72=28.
答:C点对应的数是28.
点评:本题考查的是数轴,熟知数轴上两点间距离的定义是解答此题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
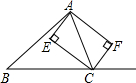 已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F.
已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F. 21、已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点.
21、已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点.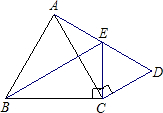 已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.
已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形. 已知:如图,E,F分别是?ABCD的边AD,BC的中点.求证:AF=CE.
已知:如图,E,F分别是?ABCD的边AD,BC的中点.求证:AF=CE. 已知,如图,BE、CF分别是△ABC的边AC、AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.请你判断线段AD与AG有什么关系?并证明.
已知,如图,BE、CF分别是△ABC的边AC、AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.请你判断线段AD与AG有什么关系?并证明.