题目内容
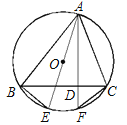
【题目】如图△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC,垂足为D.
(1)求证:BE=CF;
(2)若AB=8,AC=6,AD=5,求⊙O的半径.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由圆周角定理得出∠ABE=90°,得出∠BAE+∠BEA=90°,由AF⊥BC得出∠ACD+∠CAD=90°,由圆周角定理得出∠BEA=∠ACD,再由同圆或等圆中,相等的圆周角所对的弦相等,即可得出结论;
(2)证明△ABE∽△ADC,得出对应边成比例,求出直径AE,即可得出结论.
试题解析:(1)证明:∵AE是⊙O的直径,∴∠ABE=90°,∴∠BAE+∠BEA=90°,∵AF⊥BC,∴∠ADC=90°,∴∠ACD+∠CAD=90°,又∵∠BEA=∠ACD,∴∠BAE=∠CAD,∴BE=CF;
(2)解:∵∠ABE=∠ADC=90°,∠BEA=∠ACD,∴△ABE∽△ADC,∴![]() ,即
,即![]() ,解得:AE=
,解得:AE=![]() ,∴半径r=
,∴半径r=![]() .
.

练习册系列答案
相关题目
