Question

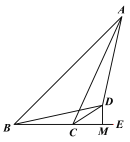
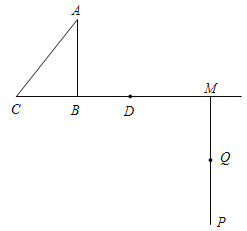
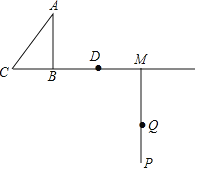
【题目】如图，在Rt△ABC中，AB＝4，BC＝3，点D从B点出发，沿射线CB方向以每秒3个单位长度的速度运动，射线MP⊥射线CB，且BM＝10，点Q从M点出发，沿射线MQ方向以每秒a个单位长度的速度运动，已知D、Q两点同时出发，运动时间为t秒．

（1）当t＝2时，△DMQ是等腰三角形，求a的值．

（2）求t为何值时，△DCA为等腰三角形．

（3）是否存在a，使得△DMQ与△ABC全等，若存在，请直接写出a的值，若不存在，请说明理由．

Answer 1

【答案】（1）a＝2；（2）t＝1，，时，△DCA为等腰三角形；（3）当△DMQ与△ABC全等时，a＝，，，．

【解析】

（1）当t＝2时，DB＝6，得到DM＝4，由于△DMQ是等腰三角形，∠DMQ＝90°，得到DM＝MQ，于是得到a＝2；

（2）①当AC＝AD时，△DCA为等腰三角形，得到BD＝BC＝3，求得t＝1，②当AC＝CD＝4时，△DCA为等腰三角形，得到BD＝1，于是得到t＝，③当AD＝CD＝3+3t时，△DCA为等腰三角形，根据勾股定理列方程即可得到t＝，

（3）当△DMQ与△ABC全等，根据全等三角形的性质即可得到结论．

（1）当t＝2时，DB＝6，

∵BM＝10，

∴DM＝4，

∵△DMQ是等腰三角形，∠DMQ＝90°，

∴DM＝MQ，

即4＝2a，

∴a＝2；

（2）①当AC＝AD时，△DCA为等腰三角形，

∵AB⊥CD，

∴BD＝BC＝3，

∴t＝1，

②当AC＝CD＝5时，△DCA为等腰三角形，

∵BC＝3，

∴BD＝1，

∴t＝，

③当AD＝CD＝3+3t时，△DCA为等腰三角形，

∵∠ABD＝90°，

∴AB2+BD2＝AD2，

即42+（3t）2＝（3+3t）2，

∴t＝，

综上所述：t＝1，，时，△DCA为等腰三角形；

（3）当△DMQ与△ABC全等，

①△DMQ≌△ABC，

∴MQ＝BC＝3，DM＝AB＝4，

∵BM＝10，

∴BD＝6或BD＝14，

∴t＝2或t＝，

∴a＝，a＝；

②△DMQ≌△CBA，

∴DM＝BC＝3，MQ＝AB＝4，

∴BD＝7或13，

∴t＝或，

∴a＝或，

综上所述：当△DMQ与△ABC全等时，a＝，，，．