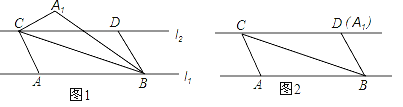题目内容
【题目】在△ABC中,AB=AC,∠BAC=45°.若AD平分∠BAC交BC于D,BE⊥AC于E,且交A于O,连接OC.则下列说法中正确的是( )①AD⊥BC;②OC平分BE;③OE=CE;④△ACD≌△BCE;⑤△OCE的周长=AC的长度

A.①②③B.②④⑤C.①③⑤D.①③④⑤
【答案】C
【解析】
①正确,利用等腰三角形的三线合一即可证明;②错误,证明OB=OC>OE即可判断;③正确,证明∠ECO=∠OBA=45°即可;④错误,缺少全等的条件;⑤正确,只要证明BE=AE,OB=OC,EO=EC即可判断.
解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD,即①正确,
∴OB=OC,
∵BE⊥AC,
∵OC>OE,
∴OB>OE,即②错误,
∵∠ABC=∠ACB,∠OBC=∠OCB,BE⊥AC,
∴∠ABE=∠ACO=45°,
∴∠ECO=∠EOC=45°,
∴OE=CE,即③正确,
∵∠AEB=90°,∠ABE=45°,
∴AE=EB,
∴△OEC的周长=OC+OE+EC=OE+OB+EC=EB+EC=AE+EC=AC,即⑤正确,
无法判断△ACD≌△BCE,故④错误,
故选:C.

练习册系列答案
相关题目