题目内容
【题目】已知R△ABDC中,∠C=90°,AD、BE是角平分线,它们相交于P,PF⊥AD于P交BC的延长线于F,交AC于H.
(1)求证:AH+BD=AB;
(2)求证:PF=PA.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)首先计算出∠APB=135°,进而得到∠BPD=45°,然后再计算出∠FPB=135°,然后证明△ABP≌△FBP,得∠F=∠CAD,然后证明△APH≌△FPD,进而得到AH=FD,再利用等量代换可得结论.
(2)由△ABP≌△FBP可得PA=PF.
证明(1)∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴∠BAD+∠ABE=![]() (∠CAB+∠CBA)=45°,
(∠CAB+∠CBA)=45°,
∴∠APB=135°,
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
在△ABP和△FBP中,
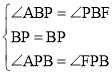 ,
,
∴△ABP≌△FBP(ASA),
∴∠BAP=∠F,
∵∠BAP=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
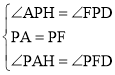 ,
,
∴△APH≌△FPD(ASA),
∴AH=FD,
又∵AB=FB,
∴AB=FD+BD=AH+BD.
(2)证明:由(1)可知△ABP≌△FBP,
∴PA=PF,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目