题目内容
 如图,已知二次函数
如图,已知二次函数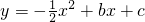 的图象经过A(2,0)、B(0,-6)两点.
的图象经过A(2,0)、B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积;
(3)若抛物线的顶点为D,在y轴上是否存在一点P,使得△PAD的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)将点A(2,0)、B(0,-6)代入得: ,
,
解得: ,
,
故这个二次函数的解析式为:y=- x2+4x-6.
x2+4x-6.
(2)∵二次函数的解析式为:y=- x2+4x-6,
x2+4x-6,
∴二次函数的对称轴为x=4,即OC=4,
∴AC=2,
故S△ABC= AC×BO=6.
AC×BO=6.
(3)存在,点P的坐标为(0, ).
).

AD长度固定,只需找到点P使AP+PD最小即可,找到点A关于y轴的对称点A',连接A'D,则A'D与y轴的交点即是点P的位置,
∵点A'与点A关于y轴对称,
∴点A'的坐标为(-2,0),
又∵顶点D的坐标为(4,2),
∴直线A'D的解析式为:y= x+
x+ ,
,
令x=0,则y= ,即点P的坐标为(0,
,即点P的坐标为(0, ).
).
分析:(1)将点A及点B的坐标代入即可得出b、c的值,继而可得出二次函数解析式;
(2)根据(1)求得的解析式,可得出对称轴,也可得出AC的长度,根据S△ABC= AC×BO可得出答案.
AC×BO可得出答案.
(3)AD长度固定,故只需找到点P使AP+PD最小即可,找到点A关于y轴的对称点A',连接A'D,则A'D与y轴的交点即是点P的位置,求出直线A'D的函数解析式,可得出点P的坐标.
点评:此题考查了二次函数综合题,涉及了待定系数法求函数解析式、三角形的面积,要注意掌握点的坐标与线段长度之间的转换,难点在第三问,注意运用轴对称的性质求最短路线.
 ,
,解得:
 ,
,故这个二次函数的解析式为:y=-
 x2+4x-6.
x2+4x-6.(2)∵二次函数的解析式为:y=-
 x2+4x-6,
x2+4x-6,∴二次函数的对称轴为x=4,即OC=4,
∴AC=2,
故S△ABC=
 AC×BO=6.
AC×BO=6.(3)存在,点P的坐标为(0,
 ).
).
AD长度固定,只需找到点P使AP+PD最小即可,找到点A关于y轴的对称点A',连接A'D,则A'D与y轴的交点即是点P的位置,
∵点A'与点A关于y轴对称,
∴点A'的坐标为(-2,0),
又∵顶点D的坐标为(4,2),
∴直线A'D的解析式为:y=
 x+
x+ ,
,令x=0,则y=
 ,即点P的坐标为(0,
,即点P的坐标为(0, ).
).分析:(1)将点A及点B的坐标代入即可得出b、c的值,继而可得出二次函数解析式;
(2)根据(1)求得的解析式,可得出对称轴,也可得出AC的长度,根据S△ABC=
 AC×BO可得出答案.
AC×BO可得出答案.(3)AD长度固定,故只需找到点P使AP+PD最小即可,找到点A关于y轴的对称点A',连接A'D,则A'D与y轴的交点即是点P的位置,求出直线A'D的函数解析式,可得出点P的坐标.
点评:此题考查了二次函数综合题,涉及了待定系数法求函数解析式、三角形的面积,要注意掌握点的坐标与线段长度之间的转换,难点在第三问,注意运用轴对称的性质求最短路线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
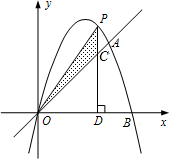 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.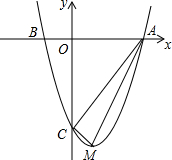 (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).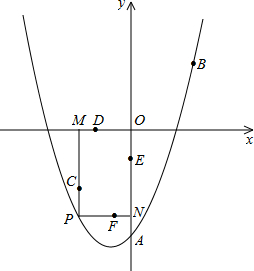 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B(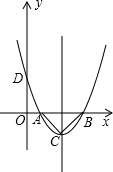 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4). 如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )
如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )