题目内容
如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.(1)求出二次函数的解析式;
(2)当点P在直线OA的上方时,求线段PC的最大值;
(3)当m>0时,探索是否存在点P,使得△PCO为等腰三角形,如果存在,求出P的坐标;如果不存在,请说明理由.
分析:(1)设y=ax(x-4),把A点坐标代入即可求出答案;
(2)根据点的坐标求出PC=-m2+3m,化成顶点式即可求出线段PC的最大值;
(3)当0<m<3时,仅有OC=PC,列出方程,求出方程的解即可;当m≥3时,PC=CD-PD=m2-3m,OC=
m,分为三种情况:①当OC=PC时,m2-3m=
m,求出方程的解即可得到P的坐标;同理可求:②当OC=OP时,③当PC=OP时,点P的坐标.综合上述即可得到答案.
(2)根据点的坐标求出PC=-m2+3m,化成顶点式即可求出线段PC的最大值;
(3)当0<m<3时,仅有OC=PC,列出方程,求出方程的解即可;当m≥3时,PC=CD-PD=m2-3m,OC=
| 2 |
| 2 |
解答:解:(1)设y=ax(x-4),
把A点坐标(3,3)代入得:
a=-1,
函数的解析式为y=-x2+4x,
答:二次函数的解析式是y=-x2+4x.
(2)解:0<m<3,PC=PD-CD,
∵D(m,0),PD⊥x轴,P在y=-x2+4x上,C在OA上,A(3,3),
∴P(m,-m2+4m),C(m,m)
∴PC=PD-CD=-m2+4m-m=-m2+3m,
=-(m-
)2+
,
∵-1<0,开口向下,
∴有最大值,
当D(
,0)时,PCmax=
,
答:当点P在直线OA的上方时,线段PC的最大值是
.
(3)当0<m<3时,仅有OC=PC,
∴-m2+3m=
m,
解得m=3-
,
∴P(3-
,1+2
);
当m≥3时,PC=CD-PD=m2-3m,
OC=
m,
由勾股定理得:OP2=OD2+DP2=m2+m2(m-4)2,
①当OC=PC时,m2-3m=
m,
解得:m=3+
或m=0(舍去),
∴P(3+
,1-2
);
②当OC=OP时,(
m)2=m2+m2(m-4)2,
解得:m1=5,m2=3,
∵m=3时,P和A重合,即P和C重合,不能组成三角形POC,
∴m=3舍去,
∴P(5,-5);
③当PC=OP时,m2(m-3)2=m2+m2(m-4)2,
解得:m=4,
∴P(4,0),
答:存在,P的坐标是(3-
,1+2
)或(3+
,1-2
)或(5,-5)或(4,0).
把A点坐标(3,3)代入得:
a=-1,
函数的解析式为y=-x2+4x,
答:二次函数的解析式是y=-x2+4x.
(2)解:0<m<3,PC=PD-CD,
∵D(m,0),PD⊥x轴,P在y=-x2+4x上,C在OA上,A(3,3),
∴P(m,-m2+4m),C(m,m)
∴PC=PD-CD=-m2+4m-m=-m2+3m,
=-(m-
| 3 |
| 2 |
| 9 |
| 4 |
∵-1<0,开口向下,
∴有最大值,
当D(
| 3 |
| 2 |
| 9 |
| 4 |
答:当点P在直线OA的上方时,线段PC的最大值是
| 9 |
| 4 |
(3)当0<m<3时,仅有OC=PC,

∴-m2+3m=
| 2 |
解得m=3-
| 2 |
∴P(3-
| 2 |
| 2 |
当m≥3时,PC=CD-PD=m2-3m,
OC=
| 2 |
由勾股定理得:OP2=OD2+DP2=m2+m2(m-4)2,
①当OC=PC时,m2-3m=
| 2 |
解得:m=3+
| 2 |
∴P(3+
| 2 |
| 2 |
②当OC=OP时,(
| 2 |
解得:m1=5,m2=3,
∵m=3时,P和A重合,即P和C重合,不能组成三角形POC,
∴m=3舍去,
∴P(5,-5);
③当PC=OP时,m2(m-3)2=m2+m2(m-4)2,
解得:m=4,
∴P(4,0),
答:存在,P的坐标是(3-
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题主要考查对用待定系数法求二次函数的解析式,等腰三角形的性质,勾股定理,二次函数的最值等知识点的理解和掌握,用的数学思想是分类讨论思想,此题是一个综合性比较强的题目,(3)小题有一定的难度.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).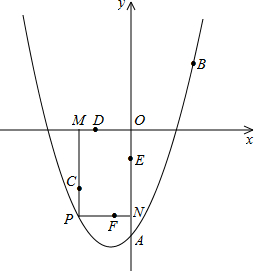 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B( 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4). 如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )
如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )