Question

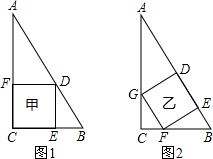
数学兴趣小组成员，为了从一张腰长为2的等腰直角三角形的纸片中剪出一个尽可能大的正方形，探究出甲、乙两种剪法（图甲、图乙）
（1）请计算说明甲、乙两种解法哪种剪出的正方形纸片更大．
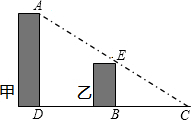
（2）李明同学想从一张直角边分别为3、4的三角形纸片中，剪出一个边长为1.7的正方形能做到吗？若能，请说明理由，并在图中用虚线画出所剪正方形；若不能，请说明不能的理由．

Answer 1

（1）如图甲所示：设正方形的边长为x，则AE=2-x，
∵DE⊥AC，BC⊥AC，
∴△ADE∽△ABC，
∴

AE

AC

=

DE

BC

，

2-x

2

=

x

2

，
解得x=1，
∴S_正方形=1；
如图乙所示：
∵等腰直角三角形的边长为2，
∴AB=

AC2+BC2

=

22+22

=2

2

，
设正方形的边长为x，则AD=

2 2 -x

2

=

2

-

x

2

，
∵∠A=∠A，∠ADE=∠ACB，
∴△ADE∽△ACB，
∴

AD

AC

=

DE

BC

，

2 - x 2

2

=

x

2

，
解得x=

2 2

3

∴S_正方形=（

2 2

3

）²=

8

9

；
∵1＞

8

9

，
∴甲种剪法面积更大；


（2）能．
如图丙所示：
设正方形的边长为x，则AE=3-x，
∵DE⊥AC，BC⊥AC，
∴△ADE∽△ABC，
∴

AE

AC

=

DE

BC

，

3-x

3

=

x

4

，
解得x=

12

7

≈1.71＞1.7，
∴剪出一个边长为1.7的正方形．