题目内容
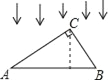
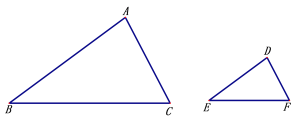
【题目】求证:相似三角形对应角的角平分线之比等于相似比.要求:
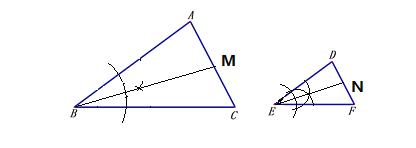
①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
【答案】见解析
【解析】
(1)按照作一个角的平分线的作法作出一组对应角的平分线即可;
(2)首先根据相似三角形的对应角相等,由△ABC∽△DEF,得出∠A=∠D ,∠ABC =∠DEF ,再根据角平分线的定义,得出∠ABM=∠DEN,根据两角分别相等,两三角形相似,证明△ABM∽△DEN,继而得出对应边的比等于相似比.
(1)
(2)如(1)图,已知△ABC∽△DEF,△ABC和△DEF的相似比为k,BM、EN分别是△ABC和△DEF的角平分线。求证:![]() =k.
=k.
证明:∵△ABC∽△DEF,,
∴∠A=∠D ,∠ABC =∠DEF ,,
∵BM、EN分别是△ABC和△DEF的角平分线,
∴∠ABM=![]() ∠ABC,∠DEN=
∠ABC,∠DEN=![]() ∠DEF,
∠DEF,
∴∠ABM=∠DEN,
∵∠A=∠D ,∠ABM=∠DEN,
∴△ABM∽△DEN,
∴![]() =k.
=k.

练习册系列答案
相关题目