题目内容
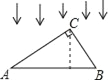
【题目】如图,在Rt△ABC中,∠C=90°,投影线方向如图所示,点C在斜边AB上的正投影为点D,
(1)试写出边AC、BC在AB上的投影;
(2)试探究线段AC、AB和AD之间的关系;
(3)线段BC、AB和BD之间也有类似的关系吗?请直接写出结论.
【答案】(1)边AC、BC在AB上的投影分别为AD、BD;(2)AC2=ADAB;(3)BC2=BDAB.
【解析】
(1)根据投影的定义求解;
(2)通过证明△ADC∽△ACB可得AC2=ADAB;
(3)通过证明△BCD∽△BAC即可得到BC2=BDAB.
解:(1)边AC、BC在AB上的投影分别为AD、BD;
(2)∵点C在斜边AB上的正投影为点D,
∴CD⊥AB,
∴∠ADC=90°,
而∠DAC=∠CAB,
∴△ADC∽△ACB,
∴AC:AB=AD:AC,
∴AC2=ADAB;
(3)与(2)一样可证△BCD∽△BAC,
则BC:AB=BD:BC,
∴BC2=BDAB.

练习册系列答案
相关题目