题目内容
【题目】如图1所示是小明设计的带菱形图案的花边作品,该作品由形如图2所示的矩形图案拼接而成(不重叠,无缝隙),小明发现图(2)具有对称之美,它既是轴对称图形,也是中心对称图形,并对这个图形进行探究.

(1)如图3,若知图案的一部分,请你根据如图2将图3的图案补充完整(要求:尺规作图,保留作图痕迹,不写作法);

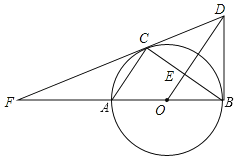
(2)如图4,![]() ,
,![]() ,上、下两个阴影部分的面积之和为
,上、下两个阴影部分的面积之和为![]() ,其内部菱形由两组距离相等的平行线两两相交得到,求该菱形的周长;
,其内部菱形由两组距离相等的平行线两两相交得到,求该菱形的周长;
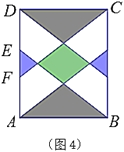
(3)小明认为:图4中的4个空白部分在一定条件下能拼成一个正方形(不重叠,无缝隙),请你帮助小明写出应满足的条件(提示:求出![]() 与
与![]() 的长度之比,并指出点
的长度之比,并指出点![]() 、
、![]() 的位置).
的位置).

【答案】(1)答案见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先做出最上方的三角形,然后将上下两个三角形的边分别延长即可;
(2)设出AB=![]() ,BC=
,BC=![]() ,表示出MN,及NP+MQ,表示出上下阴影面积之和,求得
,表示出MN,及NP+MQ,表示出上下阴影面积之和,求得![]() ,利用勾股定理求得BE,利用
,利用勾股定理求得BE,利用![]() 求得EH,MH,得菱形周长;
求得EH,MH,得菱形周长;
(3)设![]() ,
,![]() ,根据中间为正方形表示FH,AM及HM,利用
,根据中间为正方形表示FH,AM及HM,利用
![]() 计算出
计算出![]() 与
与![]() 比值即可.
比值即可.
(1)尺规作图,如图所示:

(2)∵![]() ,
,![]() ,
,
∴设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]()
![]()
解得![]() ,∴
,∴![]() ,
,![]() (舍),
(舍),
∴![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]()
又∵![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()

(3)由题意得
![]() ,
,![]() ,四边形
,四边形![]() 为直角梯形且
为直角梯形且![]()
设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]()
即![]() 即
即![]()


练习册系列答案
相关题目
【题目】已知二次函数![]() 自变量
自变量![]() 的值和它对应的函数值
的值和它对应的函数值![]() 如下表所示:
如下表所示:
| … | 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | … |
(1)点M是该二次函数图象上一点,若点M纵坐标为8时,求点M的坐标;
(2)设该二次函数图象与![]() 轴的左交点为
轴的左交点为![]() ,它的顶点为
,它的顶点为![]() ,该图象上点
,该图象上点![]() 的横坐标为4,求
的横坐标为4,求![]() 的面积.
的面积.