题目内容
观察,猜想,证明.
观察下列的等式
①2
=
;②3
=
;③4
═
…
(1)发现上述3个等式的规律,猜想第5个等式并进行验证;
(2)写出含字母n(n为任意自然数,且n≥2)表示的等式,并写出证明过程.
观察下列的等式
①2
|
2+
|
|
3+
|
|
4+
|
(1)发现上述3个等式的规律,猜想第5个等式并进行验证;
(2)写出含字母n(n为任意自然数,且n≥2)表示的等式,并写出证明过程.
考点:二次根式的性质与化简
专题:规律型
分析:(1)根据已知得出数字规律,进而验证得出即可;
(2)根据已知得出数字规律,用n表示出即可,进而验证得出.
(2)根据已知得出数字规律,用n表示出即可,进而验证得出.
解答:解:(1)猜想:6
=
,
验证:右边=
=
=
=
=6
=左边;
(2)第n-1个等式:n•
=
;
证明:
右边=
=
=
=
=n•
=左边.
|
6+
|
验证:右边=
6+
|
|
|
|
|
(2)第n-1个等式:n•
|
n+
|
证明:
右边=
n+
|
|
|
|
|
点评:此题主要考查了数字变化规律以及二次根式的性质,正确化简二次根式是解题关键.

练习册系列答案
相关题目
 如图,菱形ABCD的周长为20cm,对角线AC、BD相交于点O,AC=8cm.
如图,菱形ABCD的周长为20cm,对角线AC、BD相交于点O,AC=8cm.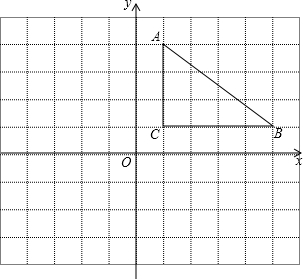 如图,△ABC三点的坐标分别为A(1,4)、B(5,1)、C(1,1).
如图,△ABC三点的坐标分别为A(1,4)、B(5,1)、C(1,1). 已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点.
已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点. 如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F,线段DF与图中的哪一条线段相等?先将猜想出的结论填写在下面的横线上,然后再加以证明.即DF=
如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F,线段DF与图中的哪一条线段相等?先将猜想出的结论填写在下面的横线上,然后再加以证明.即DF=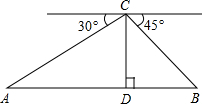 如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为50m,点A、D、B在同一条直线上,则A、B两点的距离是
如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为50m,点A、D、B在同一条直线上,则A、B两点的距离是