题目内容
 已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点.
已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点.①求证:EF与GH互相平分;
②当四边形ABCD的边满足
考点:中点四边形
专题:证明题
分析:(1)连接GE、GF、HF、EH,根据三角形的中位线定理即可证得EG=FH/GF=EH,则四边形EFGH是平行四边形,
利用平行四边形的性质即可证得;
(2)EF⊥GH时能得到四边形GFHE四边相等,从而得到四边形ABCD的四边相等.
利用平行四边形的性质即可证得;
(2)EF⊥GH时能得到四边形GFHE四边相等,从而得到四边形ABCD的四边相等.
解答: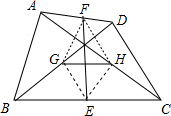 解:(1)连接GE、GF、HF、EH.
解:(1)连接GE、GF、HF、EH.
∵E、G分别是AD、BD的中点,
∴EG=
CD,
同理FH=
CD,FG=
AB,EH=
AB
∴EG=FH、GF=EH
∴四边形EFGH是平行四边形.
∴EF与GH互相平分;
(2)当EF⊥GH时四边形EFGH是菱形,
此时GF=FH=HE=EG,
∵EG=
CD,FH=
CD,FG=
AB,EH=
AB
∴AB=BC=CD=DA,
∴当四边形ABCD的边满足条件AB=BC=CD=DA时,EF⊥GH.
 解:(1)连接GE、GF、HF、EH.
解:(1)连接GE、GF、HF、EH.∵E、G分别是AD、BD的中点,
∴EG=
| 1 |
| 2 |
同理FH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EG=FH、GF=EH
∴四边形EFGH是平行四边形.
∴EF与GH互相平分;
(2)当EF⊥GH时四边形EFGH是菱形,
此时GF=FH=HE=EG,
∵EG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=BC=CD=DA,
∴当四边形ABCD的边满足条件AB=BC=CD=DA时,EF⊥GH.
点评:本题考查了三角形的中位线定理,菱形的判定与性质,正确证明四边形EFGH是菱形是关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.
如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点. 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.