Question

【题目】如图 所示,用 20 m 的篱笆(细线部分)，两面靠墙围成矩形的苗圃.

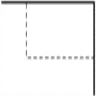
(1)设矩形的一边长为x(m),面积为y(m 2 )，求y关于x的函数表达式；

(2)求当x取8、9、10、11、12时y的值，并观察这几种情况下，哪种情况面积最大？

Answer 1

【答案】(1)y=x(20-x)； (2)当x=8、9、10、11、12时，y=96、99、100、99、96； 当x取10时得到的面积大.

【解析】试题分析：（1）根据矩形的邻边之和为20以及其中一边长为x，表示出另一边长，然后利用矩形的面积公式列出矩形面积y与x的关系式即可；

（2）分别将数值代入进行计算，然后进行比较即可得.

试题解析：（1）由题意得：y=x(20-x)；

（2）x=8时，y=8×(20-8)=96，

x=9时，y=9×(20-9)=99，

x=10时，y=10×(20-10)=100，

x=11时，y=11×(20-11)=99，

x=12时，y=12×(20-12)=96，

观察可知当x=10时，得到的面积最大.