题目内容
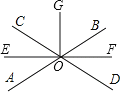
【题目】如图,直线AB,CD相交于点O,OE,OF,OG分别是∠AOC,∠BOD,∠BOC的平分线,以下说法不正确的是( )
A.∠DOF与∠COG互为余角
B.∠COG与∠AOG互为补角
C.射线OE,OF不一定在同一条直线上
D.射线OE,OG互相垂直
【答案】C
【解析】
首先根据角平分线的性质得出∠COE=![]() ∠AOC,∠DOF=∠BOF=
∠AOC,∠DOF=∠BOF=![]() ∠BOD,进而得出∠COE=∠BOF,∠COG=∠BOG,可判定∠DOF与∠COG互为余角;射线OE,OG互相垂直;然后根据∠AOG+∠BOG=180°,得出∠AOG+∠COG=180°,可判定∠COG与∠AOG互为补角,又由∠EOG+∠FOG=180°,得出射线OE,OF一定在同一条直线上,即可得解.
∠BOD,进而得出∠COE=∠BOF,∠COG=∠BOG,可判定∠DOF与∠COG互为余角;射线OE,OG互相垂直;然后根据∠AOG+∠BOG=180°,得出∠AOG+∠COG=180°,可判定∠COG与∠AOG互为补角,又由∠EOG+∠FOG=180°,得出射线OE,OF一定在同一条直线上,即可得解.
∵∠AOC=∠BOD,
∵OE,OF分别是∠AOC,∠BOD的平分线,
∴∠COE=![]() ∠AOC,∠DOF=∠BOF=
∠AOC,∠DOF=∠BOF=![]() ∠BOD,
∠BOD,
∴∠COE=∠BOF,
∵OG是BOC的平分线,
∴∠COG=∠BOG,
∴∠COE+∠COG=∠BOF+∠BOG=![]() ×180°=90°,
×180°=90°,
∴∠EOG=∠FOG=90°,
∴∠DOF与∠COG互为余角;故A正确;射线OE,OG互相垂直;故D正确;
∵∠AOG+∠BOG=180°,
∴∠AOG+∠COG=180°,
∴∠COG与∠AOG互为补角,故B正确;
∵∠EOG+∠FOG=180°,
∴射线OE,OF一定在同一条直线上,故C错误.
故选:C.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复上述过程,下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.64 | 0.58 | 0.605 | 0.601 |
(1)请将表中的数据补充完整,
(2)请估计:当n很大时,摸到白球的概率约是 .(精确到0.1)