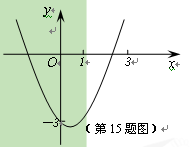
题目内容
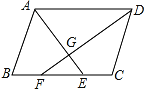
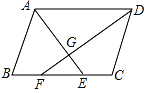
【题目】如图,在ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.
(1)求证:∠AGD=90°.
(2) 求证:BF=CE.
【答案】(1)见详解;(2)见详解
【解析】
(1)由平行四边形的性质和角平分线的定义即可得出结论;
(2)根据平行四边形的性质和平行线的性质推出∠ADF=∠CFD,结合∠ADF=∠CDF求出CD=CF,同理可得AB=BE,即可证明BF=CE.
解:(1)∵四边形ABCCD是平行四边形,
∴∠BAD+∠ADC=180°,
∵AE、DF分别是∠BAD、∠ADC的平分线,
∴∠DAG=![]() ∠BAD,∠ADG=
∠BAD,∠ADG=![]() ∠ADC,
∠ADC,
∴∠DAG+∠ADG=![]() ×(∠BAD+∠ADC)=
×(∠BAD+∠ADC)=![]() ×180°=90°,
×180°=90°,
∴∠AGD=90°;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠CFD,
∵∠ADF=∠CDF,
∴∠CDF=∠CFD,
∴CD=CF
同理可得AB=BE,
∵AB=CD,
∴CF=BE,
∵BE=BF+EF,CF=CE+EF
∴BF=CE.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案【题目】九年级二班![]() 名同学在“爱心捐款”活动中,捐款情况统计如表,
名同学在“爱心捐款”活动中,捐款情况统计如表,
捐款金额(元) |
|
|
|
|
|
捐款人数(人) |
|
|
|
|
|
![]() 表中
表中![]() ________;
________;
![]() 二班同学捐款数组成的数据中,中位数是________、众数是________;
二班同学捐款数组成的数据中,中位数是________、众数是________;
![]() 九年级二班
九年级二班![]() 名同学平均捐款多少元?
名同学平均捐款多少元?
![]() 根据样本数据,估计该校九年级
根据样本数据,估计该校九年级![]() 名学生在本次活动中捐款多于
名学生在本次活动中捐款多于![]() 元的人数.
元的人数.
【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
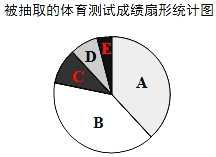
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.