题目内容
 如图,等腰△ABC中,AB=AC,D是BC上一点,且AD=BD.
如图,等腰△ABC中,AB=AC,D是BC上一点,且AD=BD.
(1)试说明:△ABC∽△DBA;
(2)若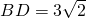 ,
,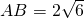 ,求BC的长;
,求BC的长;
(3)若 ,求∠C的度数.
,求∠C的度数.
解:(1)∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠DAB,
∴∠B=∠C=∠DAB,
∴△ABC∽△DBA;
(2)∵△ABC∽△DBA,
∴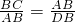 ,
,
即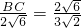 ,
,
∴ ;
;
(3)设AD=a,则BC=3a,BD=a,
作AH⊥BC于点H,则H为BC的中点,
∴DH=BH-BD=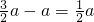 ,
,
在Rt△ADH中, ,
,
∴∠ADH=60°,
∵∠B+∠BAD=∠ADH,∠B=∠BAD,
∴∠B=30°,
∴∠C=∠B=30°.
分析:(1)由等边对等角,可得∠B=∠C,∠B=∠DAB,即可求得△ABC∽△DBA;
(2)由相似三角形的对应边成比例,即可求得BC的长;
(3)由三角函数的性质,可求得∠B的值,即可求得∠C的值.
点评:此题考查了等腰三角形中的等边对等角定理,以及相似三角形的判定与性质和三角函数的性质.此题综合性较强,但难度不大,解题时要注意细心.
∴∠B=∠C,∠B=∠DAB,
∴∠B=∠C=∠DAB,
∴△ABC∽△DBA;
(2)∵△ABC∽△DBA,
∴
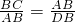 ,
,
即
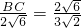 ,
,∴
 ;
;(3)设AD=a,则BC=3a,BD=a,
作AH⊥BC于点H,则H为BC的中点,
∴DH=BH-BD=
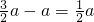 ,
,在Rt△ADH中,
 ,
,∴∠ADH=60°,
∵∠B+∠BAD=∠ADH,∠B=∠BAD,
∴∠B=30°,
∴∠C=∠B=30°.
分析:(1)由等边对等角,可得∠B=∠C,∠B=∠DAB,即可求得△ABC∽△DBA;
(2)由相似三角形的对应边成比例,即可求得BC的长;
(3)由三角函数的性质,可求得∠B的值,即可求得∠C的值.
点评:此题考查了等腰三角形中的等边对等角定理,以及相似三角形的判定与性质和三角函数的性质.此题综合性较强,但难度不大,解题时要注意细心.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
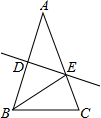 如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )| A、80° | B、70° | C、60° | D、50° |
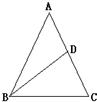 13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为
13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为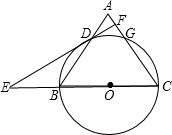 如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE=
如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE=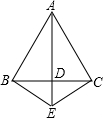 如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点.
如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点.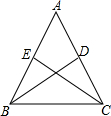 如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.
如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.