题目内容
已知等腰△ABC中，AB=AC，BC=4，内切圆的半径为1，则腰长为分析：先画图，由△AOD∽△ACE，则
=
，从而得出AC=2AO，设AO=x，则AC=2x，再由勾股定理求得x，则可得出AC．
| OD |
| AO |
| CE |
| AC |
解答：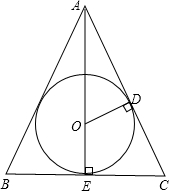
解：如图，∵AB=AC，BC=4，∴CE=2，
∴△AOD∽△ACE，∴
=
，
∴AC=2AO，
设AO=x，则AC=2x，
∵OD=OE=1，
∴由勾股定理求得，（x+1）2+22=4x2，
解得x=
，
∴AC=
，
故答案为
．
解：如图，∵AB=AC，BC=4，∴CE=2，∴△AOD∽△ACE，∴
| OD |
| AO |
| CE |
| AC |
∴AC=2AO，
设AO=x，则AC=2x，
∵OD=OE=1，
∴由勾股定理求得，（x+1）2+22=4x2，
解得x=
| 5 |
| 3 |
∴AC=
| 10 |
| 3 |
故答案为
| 10 |
| 3 |
点评：本题考查了三角形的内切圆和相似三角形的判定和性质，是基础知识要熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目
24、（1）如图，△ABC纸片中，∠A=36°，AB=AC，请你剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形．请画出示意图，并标明必要的角度；
12、如图：已知等腰△ABC中，腰AB=AC=13cm，底BC=24cm，求△ABC的面积．