题目内容
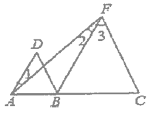
【题目】已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且![]() =
=![]() =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
=m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
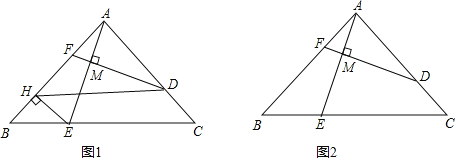
(1)如图1,过点E作EH⊥AB于点H,连结DH.
①求证:四边形DHEC是平行四边形;
②若m=![]() ,求证:AE=DF;
,求证:AE=DF;
(2)如图2,若m=![]() ,求
,求![]() 的值.
的值.
【答案】(1)①证明见解析;②证明见解析;(2)![]()
【解析】(1)①先判断出△BHE∽△BAC,进而判断出HE=DC,即可得出结论;
②先判断出AC=AB,BH=HE,再判断出∠HEA=∠AFD,即可得出结论;
(2)先判断出△EGB∽△CAB,进而求出CD:BE=3:5,再判断出∠AFM=∠AEG进而判断出△FAD∽△EGA,即可得出结论.
(1)①证明:∵EH⊥AB,∠BAC=90°,
∴EH∥CA,
∴△BHE∽△BAC,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴HE=DC,
∵EH∥DC,
∴四边形DHEC是平行四边形;
②∵![]() ,∠BAC=90°,
,∠BAC=90°,
∴AC=AB,
∵![]() ,HE=DC,
,HE=DC,
∴HE=DC,
∴![]() ,
,
∵∠BHE=90°,
∴BH=HE,
∵HE=DC,
∴BH=CD,
∴AH=AD,
∵DM⊥AE,EH⊥AB,
∴∠EHA=∠AMF=90°,
∴∠HAE+∠HEA=∠HAE+∠AFM=90°,
∴∠HEA=∠AFD,
∵∠EHA=∠FAD=90°,
∴△HEA≌△AFD,
∴AE=DF;
(2)如图,过点E作EG⊥AB于G,
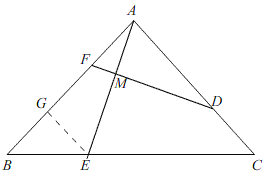
∵CA⊥AB,
∴EG∥CA,
∴△EGB∽△CAB,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴EG=CD,
设EG=CD=3x,AC=3y,
∴BE=5x,BC=5y,
∴BG=4x,AB=4y,
∵∠EGA=∠AMF=90°,
∴∠GEA+∠EAG=∠EAG+∠AFM,
∴∠AFM=∠AEG,
∵∠FAD=∠EGA=90°,
∴△FAD∽△EGA,
∴![]() .
.

【题目】某市民广场地面铺设地砖,决定采用黑白2种地砖,按如下方案铺设,首先在广场中央铺2块黑色砖(如图①),然后在黑色砖的四周铺上白色砖(如图②),再在白色砖的四周铺上黑色砖(如图③),再在黑色砖的四周铺上白色砖(如图④),这样反复更换地砖的颜色,按照这种规律,直至铺满整个广场,观察下图,解决下列问题.
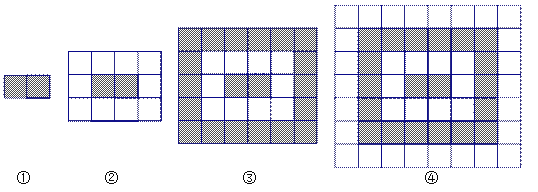
(1)填表
图形序号数 | ① | ② | ③ | ④ | … |
地砖总数(包括黑白地砖) | 2 |
(2)按照这种规律第6个图形一共用去地砖多少块?
(3)按照这种规律第![]() 个图形一共用去地砖多少块?(用含
个图形一共用去地砖多少块?(用含![]() 的代数式表示)
的代数式表示)