题目内容
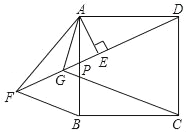
【题目】如图,两条宽度都是3cm的纸条交错地叠在一起,相交成∠α=60°.
(1)试判断重叠部分的四边形的形状;
(2)求重叠部分的面积.
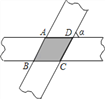
【答案】(1)重叠部分的四边形是菱形,理由见解析;(2)3![]()
【解析】试题分析:(1)根据两组对边分别平行可先判定重叠四边形是平行四边形,通过作高,利用高相等证明三角形全等可证平行四边形的邻边相等,继而证明菱形,(2)根据特殊角的直角三角形的性质,30度角所对直角边等于斜边的一半性质可利用纸条的宽求出菱形的边长,根据菱形面积公式计算即可.
试题解析:(1)重叠部分的四边形是菱形,
理由如下:∵两纸条对边平行,
∴AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,
∴∠B=∠D,
过点A作AE⊥BC于E,作AF⊥CD于F,则AE=AF=3,
在△ABE和△ADF中,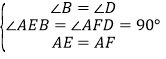 ,
,
∴△ABE≌△ADF(AAS),
∴AB=AD,
∴ABCD是菱形,即:重叠部分的四边形是菱形,
(2)如图,∠ADF=60°,∠DAF=30°,
∴AD=2DF,由勾股定理得DF=![]() ,
,
∵重叠部分的四边形是菱形,
∴重叠部分的面积=![]() ×3÷2=
×3÷2=![]() .
.

【题目】为了解上一次八年级数学测验成绩情况,随机抽取了40名学生的成绩进行统计分析,这40名学生的成绩数据如下:
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
(1)将样本数据适当分组,制作频数分布表:
分 组 |
|
|
|
|
|
频 数 |
|
|
|
|
|
(2)根据频数分布表,绘制频数直方图:
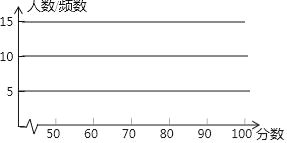
(3)从图可以看出,这40名学生的成绩都分布在什么范围内?分数在哪个范围的人数最多?