题目内容
【题目】如图，A（0，8）是直角坐标系y轴上一点，动点P从原点O出发，沿x轴正半轴运动，速度为每秒1个单位长度，以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
(1)若AB∥x轴，求t的值；
(2)当t=6时，坐标平面内有一点M（不与A重合），使得以M、P、B为顶点的三角形和△ABP全等，请直接写出点M的坐标；
(3)在（2）的条件下，在x轴上是否存在点D，使O、A、B、D为顶点的四边形面积是104？如果存在，请求出点D的坐标，如果不存在，请说明理由；
(4)设点A关于x轴的对称点为A，连接A′B，在点P运动的过程中∠OA′B的度数是否会发生变化，若不变，请求出∠OA′B的度数，若改变，请说明理由.
【答案】(1) t的值为
秒；(2) 点M的坐标为：（12，﹣8），（8，14），（14，﹣2）；(3) 存在，点D的坐标为：（18，0）或（
，0）；(4)∠OA'B=45°，不发生变化；理由见解析.
【解析】
(1)根据
是等腰直角三角形以及AB∥
轴，求得∠APO为直角，证得
也是等腰直角三角形，从求得答案；
(2)分类讨论：分别讨论当△ABP≌△MBP、△ABP≌△MPB、△ABP≌△MPB时，点M的坐标的情况；过点M作x轴的垂线、过点B作y轴的垂线，利用等腰直角三角形的性质及全等三角形的判定和性质求得点M的坐标即可.
(3)分类讨论：①D在x轴的正半轴上；②D在x轴的负半轴上，根据面积的和差，列式计算可得答案．
(4)根据已知条件易证△PAO≌△BPC，利用全等三角形的性质结合点A、点B的坐标，可求得点B的坐标，可证得点B在直线
上，再根据点A关于x轴的对称点为
（0，-8）也在直线上，从而求得∠OA′B的度数.
(1) ∵是以P为直角顶点的等腰直角三角形，
∴
，
∵AB∥轴，
∴
，
∴为等腰直角三角形，
∴
，
∴
(秒)，
故t的值为秒；
(2)当t＝6时，M、P、B为顶点的三角形和△ABP全等，
①如下图，若△ABP≌△MBP，
则AP＝PM，过点M作MD⊥OP于点D，
在△AOP和△MDP中，
，
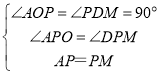∴△AOP≌△MDP（AAS），
∴OA＝DM＝8，OP＝PD＝6，
∴M的坐标为：（12，-8）．
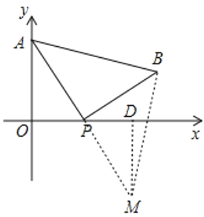
②如下图，若△ABP≌△MPB，则
，
过点M作M
⊥x轴于点，过点
作
⊥x轴于点
，过点作
⊥
轴于点
，
∵△APB为等腰直角三角形，则△MPB也为等腰直角三角形，
∴∠BAP＝∠MPB=45
，
∵△APB为等腰直角三角形，
∴∠3+∠2=180°-90°=90°．
又∵∠1+∠3=90°，
∴∠1=∠2．
在△PAO和△BPE中，
，
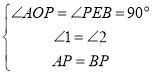∴△PAO≌△BPE（AAS），
∴
∵⊥x轴
⊥轴
∴四边形
为矩形，
∴
，则
在
和
中
∠BAF＝45+
，∠MPE＝45+
，
∴∠BAF＝∠MPE
在和中
∴
∴
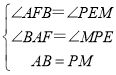
∴M的坐标为：（8，14），
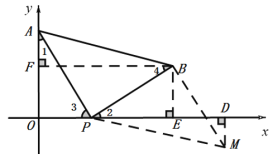
③如下图，若△ABP≌△MPB，则，
过点M作M
⊥x轴于点，过点作
⊥x轴于点，过点作⊥轴于点，
∵△APB为等腰直角三角形，则△MPB也为等腰直角三角形，
∴∠BAP＝∠MPB=45，
∵△APB为等腰直角三角形，
∴∠3+∠2=180°-90°=90°．
又∵∠1+∠3=90°，
∴∠1=∠2．
在△PAO和△BPE中，
，
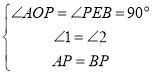∴△PAO≌△BPE（AAS），
∴
∵⊥x轴⊥轴
∴四边形
为矩形，
∴，则
∵⊥轴
∴
∵
∴
在和
中
∴
∴
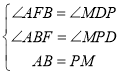
∴M的坐标为：（14，﹣2）．
综合以上可得点M的坐标为：（12，﹣8），（8，14），（14，﹣2）；
(3) 存在，
①D在x轴的正半轴上，设D（a，0），作BE⊥x轴于E点，如下图：
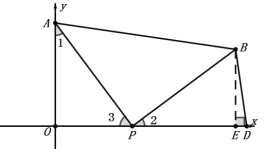
∵△APB为等腰直角三角形，
∴∠3+∠2=180°-90°=90°．
又∵∠1+∠3=90°，
∴∠1=∠2．
在△PAO和△BPE中，
，
∴△PAO≌△BPE（AAS），
∴
∵BE⊥x轴
∴BE∥AO，
∴
,
∵四边形AOBD的面积是104，
∴点D在点的右侧，
∴
，
∴
，
∴点D的坐标为：（18，0）.
②D在x轴的负半轴上，如下图：
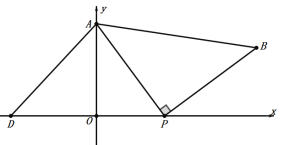
根据上面所求得的数据得：
，
∴
，
∴点D的坐标为：（，0）.
综上：点D的坐标为：（18，0）或（，0）；
(4)∠OA'B=45°，不发生变化；理由如下：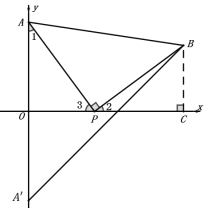
∵△APB为等腰直角三角形，
∴∠3+∠2=180°-90°=90°．
又∵∠1+∠3=90°，
∴∠1=∠2．
在△PAO和△BPC中，
，
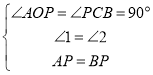∴△PAO≌△BPC（AAS），
∴AO=PC，BC=PO．
∵点A（0，8），点P（t，0）
∴PC=AO=8，BC=PO=t，CO=PC+PO=8+t
∴点B（8+t，t）；
∴点B在直线上
又∵点A关于x轴的对称点为（0，-8）也在直线上，
∴∠OA'B=45°．
