题目内容
15、如图所示，矩形ABCD的对角线相交于O，AE平分∠BAD，交BC于E，∠CAE=15°，那么∠AOB=60°
．分析：根据∠CAE=15°和AE平分∠BAD，即可求得∠BAO=60°，再根据OA=OB即可判定△ABO为等边三角形，即可求∠AOB，即可解题．
解答：解：∵∠CAE=15°和AE平分∠BAD
∴∠BAO=45°+15°=60°，
又∵AO=BO，
∴△ABO为等边三角形，
∴∠AOB=60°，
故答案为 60°．
∴∠BAO=45°+15°=60°，
又∵AO=BO，
∴△ABO为等边三角形，
∴∠AOB=60°，
故答案为 60°．
点评：本题考查了矩形对角线相等且互相平分的性质，考查了等边三角形的判定和等边三角形各内角为60°的性质，本题中求证△ABO为等边三角形是解题的关键．
练习册系列答案
相关题目
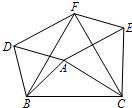18、如图所示，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABD，等边△ACE、等边△BCF．
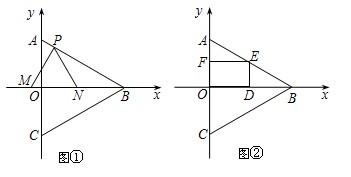
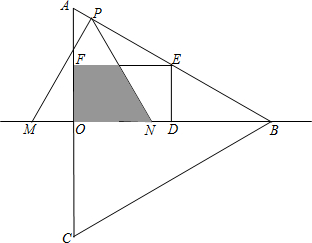边在△AOB内部作如图所示的矩形ODEF，点E在线段AB上．
（2012•邵阳）如图所示，在△ABC中，AB=AC，∠A＜90°，边BC、CA、AB的中点分别是D、E、F，则四边形AFDE是（ ）