题目内容
如图,点B在AD上,AC=CB,CD=CE,∠ACB=∠DCE=90°.试判断线段AD和BE的大小和位置关系,并给予证明.
【答案】分析:根据已知条件证明△ACD≌△BCE(SAS);然后由全等三角形的性质:对应边与对应角相等求得AD=BE,∠EBC=∠DAC=45°,所以∠ABE=90°,即AD⊥BE.
解答: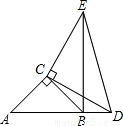 AD=BE,且AD⊥BE.
AD=BE,且AD⊥BE.
证明:∵AC=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠A=∠ABC=∠CBE=∠CEB=45°;∠ACD=∠BCE,
在△ACD和△BCE中,
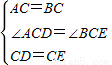 ,
,
∴△ACD≌△BCE(SAS);
∴AD=BE(全等三角形的对应边相等),
∠EBC=∠DAC=45°(全等三角形的对应角相等),
∴∠ABE=∠EBC+∠ABC=90°,
∴AD⊥BE.
点评:本题考查了全等三角形的判定与性质.解答AD⊥BE的关键是利用等腰直角三角形的性质求得∠EBC=∠DAC=45°.
解答:
 AD=BE,且AD⊥BE.
AD=BE,且AD⊥BE.证明:∵AC=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠A=∠ABC=∠CBE=∠CEB=45°;∠ACD=∠BCE,
在△ACD和△BCE中,
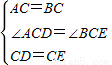 ,
,∴△ACD≌△BCE(SAS);
∴AD=BE(全等三角形的对应边相等),
∠EBC=∠DAC=45°(全等三角形的对应角相等),
∴∠ABE=∠EBC+∠ABC=90°,
∴AD⊥BE.
点评:本题考查了全等三角形的判定与性质.解答AD⊥BE的关键是利用等腰直角三角形的性质求得∠EBC=∠DAC=45°.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
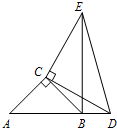 17、如图,点B在AD上,AC=CB,CD=CE,∠ACB=∠DCE=90°.试判断线段AD和BE的大小和位置关系,并给予证明.
17、如图,点B在AD上,AC=CB,CD=CE,∠ACB=∠DCE=90°.试判断线段AD和BE的大小和位置关系,并给予证明.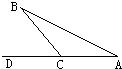
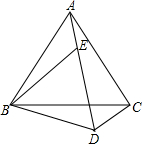 如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.
如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.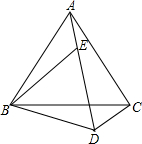 如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.
如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.