题目内容
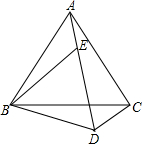 如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.
如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.分析:首先证明△ABE≌△CBD,进而得到DC=AE,再由AD=AE+ED利用等量代换AD=BD+CD.
解答:解:BD+CD=AD;
∵△ABC和△BDE都是等边三角形,
∴AB=AC,EB=DB=ED,∠ABC=∠EBD=60°,
∴∠ABC-∠EBC=∠EBD-∠EBC,
即∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴DC=AE,
∵AD=AE+ED,
∴AD=BD+CD.

∵△ABC和△BDE都是等边三角形,
∴AB=AC,EB=DB=ED,∠ABC=∠EBD=60°,
∴∠ABC-∠EBC=∠EBD-∠EBC,
即∠ABE=∠CBD,
在△ABE和△CBD中,
|
∴△ABE≌△CBD(SAS),
∴DC=AE,
∵AD=AE+ED,
∴AD=BD+CD.
点评:此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
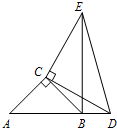 17、如图,点B在AD上,AC=CB,CD=CE,∠ACB=∠DCE=90°.试判断线段AD和BE的大小和位置关系,并给予证明.
17、如图,点B在AD上,AC=CB,CD=CE,∠ACB=∠DCE=90°.试判断线段AD和BE的大小和位置关系,并给予证明.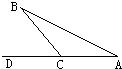
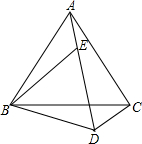 如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.
如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.