题目内容
 (1998•四川)已知一次函数y=kx+4的图象分别与直线x=2和x=6交于点A、B,且y随x的增大而增大,直线x=2和x=6又分别与x轴交于点D、C.
(1998•四川)已知一次函数y=kx+4的图象分别与直线x=2和x=6交于点A、B,且y随x的增大而增大,直线x=2和x=6又分别与x轴交于点D、C.(1)要使四边形ABCD的面积大于6,且小于64,试求k的取值范围;
(2)设一次函数y=kx+4的图象与x轴相交于点E,△BCE的外心P在第一象限,且到x轴与y轴的距离的和为6,求这个一次函数的解析式,并在直角坐标系内画出草图.
分析:(1)将x=2,x=6分别代入y=kx+4求出DA、CB,再根据梯形的面积公式求出梯形的面积;
(2)作OF⊥x轴于F,OG⊥y轴于G,根据CF=FE和O到x轴和y轴的距离之和为6,列出方程组求出k的值.
(2)作OF⊥x轴于F,OG⊥y轴于G,根据CF=FE和O到x轴和y轴的距离之和为6,列出方程组求出k的值.
解答: 解:如图,
解:如图,
(1)当x=2时,DA=2k+4,当x=6时,BC=6k+4,S四边形ABCD=CD(AD+BC)=4(2k+4)(6k+4)=16k+16,
∵四边形ABCD的面积大于6,且小于64,
∴6<16k+16<64,
∴-
<k<3;
(2)作OF⊥x轴于F,OG⊥y轴于G,
设O点坐标为(x,y),则O(x,kx+4),
根据垂径定理可知,CF=FE,
则有6-x=x-(-
),
又∵O到x轴和y轴的距离之和为6,
∴x+kx+4=6,
组成方程组为
,
整理,得3k2-k-2=0,
解得k1=1,k2=-
.
由于y随x的增大而增大,则k=1,函数解析式为y=x+4.
 解:如图,
解:如图,(1)当x=2时,DA=2k+4,当x=6时,BC=6k+4,S四边形ABCD=CD(AD+BC)=4(2k+4)(6k+4)=16k+16,
∵四边形ABCD的面积大于6,且小于64,
∴6<16k+16<64,
∴-
| 5 |
| 8 |
(2)作OF⊥x轴于F,OG⊥y轴于G,
设O点坐标为(x,y),则O(x,kx+4),
根据垂径定理可知,CF=FE,
则有6-x=x-(-
| 4 |
| k |
又∵O到x轴和y轴的距离之和为6,
∴x+kx+4=6,
组成方程组为
|
整理,得3k2-k-2=0,
解得k1=1,k2=-
| 2 |
| 3 |
由于y随x的增大而增大,则k=1,函数解析式为y=x+4.
点评:本题考查了一次函数与圆相结合的问题,同时涉及垂径定理、梯形的面积公式等问题,综合性较强.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
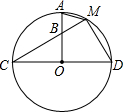 (1998•四川)已知:如图⊙O中,CD为直径,半径OA⊥CD,点B在OA上,延长CB交⊙O于点M,
(1998•四川)已知:如图⊙O中,CD为直径,半径OA⊥CD,点B在OA上,延长CB交⊙O于点M,