题目内容
如图,以等边△OAB的边OB所在直线为x轴,点O为坐标原点,使点A在第一象限建立平面直角坐标系,其中△OAB边长为4个单位,点P从O点出发沿折线OAB向B点以2个单位/秒的速度向终点B点运动,点Q从B点出发以1个单位/秒的速度向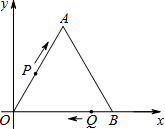 终点O点运动,两个点同时出发,运动时间为t(秒).
终点O点运动,两个点同时出发,运动时间为t(秒).
(1)请用t表示点P的坐标
(2)当t=
时,PQ⊥OA;当t=
时,PQ⊥AB;当t=
(3)△OPQ面积为S,求S关于t的函数关系式并指出S的最大值;
(4)若直线PQ将△OAB分成面积比为3:5两部分?求此时直线PQ的解析式;若不能,请说明理由.
 终点O点运动,两个点同时出发,运动时间为t(秒).
终点O点运动,两个点同时出发,运动时间为t(秒).(1)请用t表示点P的坐标
(t,
t)或(t,4
-
t)
| 3 |
| 3 |
| 3 |
(t,
t)或(t,4
-
t)
和点Q的坐标| 3 |
| 3 |
| 3 |
(4-t,0)
(4-t,0)
,其中t的取值范围是0≤t≤2或2<t≤4
0≤t≤2或2<t≤4
;(2)当t=
| 4 |
| 5 |
| 4 |
| 5 |
| 16 |
| 5 |
| 16 |
| 5 |
2
2
时,PQ⊥OB;(3)△OPQ面积为S,求S关于t的函数关系式并指出S的最大值;
(4)若直线PQ将△OAB分成面积比为3:5两部分?求此时直线PQ的解析式;若不能,请说明理由.
分析:(1)当P在OA上,即0≤t≤2;当P在AB上,即2<t≤4,分别过P作x轴的垂线,利用含30°的直角三角形三边的关系即可得到P点坐标;
(2)当PQ⊥AB,即∠OQP=30°,利用含30°的直角三角形三边的关系得到OQ=2OP,即4-t=2•2t;当PQ⊥AB,同理得到BQ=2PB,即t=2(8-2t);当PQ⊥OB,由(1)得P点和Q点的横坐标总是相等的,得到OQ=BQ,即4-t=t;分别解出t的值即可;
(3)分类讨论:当0≤t≤2时,S=
•(4-t)•
t=-
t2+2
t;当2<t≤4时,S=
•(4
-
t)•(4-t)=
(t-4)2,然后根据二次函数的最值问题即可得到S的最大值;
(4)讨论:①当P在OA、Q在OB上,即0≤t≤2时,若S△OPQ=
S△AOB;若S△OPQ=
S△AOB,分别建立方程,解方程求出t的值,确定P与Q的坐标,然后利用待定系数法求直线PQ的解析式;②同样的方法去求当P在AB、Q在OB上,即2<t≤4时,P与Q的坐标.
(2)当PQ⊥AB,即∠OQP=30°,利用含30°的直角三角形三边的关系得到OQ=2OP,即4-t=2•2t;当PQ⊥AB,同理得到BQ=2PB,即t=2(8-2t);当PQ⊥OB,由(1)得P点和Q点的横坐标总是相等的,得到OQ=BQ,即4-t=t;分别解出t的值即可;
(3)分类讨论:当0≤t≤2时,S=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
(4)讨论:①当P在OA、Q在OB上,即0≤t≤2时,若S△OPQ=
| 3 |
| 8 |
| 5 |
| 8 |
解答: 解:(1)如图1,当P在OA上,即0≤t≤2时,过点P作PD⊥x轴,
解:(1)如图1,当P在OA上,即0≤t≤2时,过点P作PD⊥x轴,
∵OP=2t,△AOB是等边三角形,
∴OD=OP•cos∠AOB=2t•
=t,PD=OP•sin60°=2t•
=
t,
∴P(t,
t);
当P在AB上,即2<t≤4时,过点P作PE⊥x轴,
∵OA+AB=8,
∴BP=8-2t,
∴BE=
=4-t,PE=4
-
t,
∴P(t,4
-
t);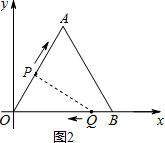
∵OB=4,
∴OE=4-t,
∴Q(4-t,0),
故答案为:(t,
t)或(t,4
-
t),(4-t,0),0≤t≤2或2<t≤4;
(2)如图2,当PQ⊥AO时,
∵∠AOB=60°,
∴∠OQP=30°,
∵OP=2t,OQ=4-t,
∴OQ=2OP,即4-t=2•2t,解得t=
;
如图3,当PQ⊥AB,
∵∠ABO=60°,
∴∠PQB=30°,
∵BP=8-2t,BQ=t,
∴BQ=2PB,即t=2(8-2t),解得t=
;
如图4,当PQ⊥OB,
由(1)得P点和Q点的横坐标总是相等的,
∴OQ=BQ,即4-t=t,解得t=2;
故答案为:
;
;2;
(3)①∵当0≤t≤2时,S=
•(4-t)•
t=-
t2+2
t,
∴当t=-
=2时,S有最大值,其最大值=
=2
;
②当2<t≤4时,S=
•(4
-
t)•(4-t)=
(t-4)2,
∴在2<t≤4范围内,S随t的增大而减小,并且当t=2时,S的最大值为2
,
∴2<t≤4时,S<2
;
综上所述,当t=2时,S有最大值2
;
(4)如图4,∵AQ=OAsin60°=4×
=2
,
∴S△AOB=
OB•AQ=
×4×2
=4
,
①当P在OA、Q在OB上,即0≤t≤2时,
∵S△OPQ=
S△AOB,
∴-
t2+2
=
,
解得t=1或3(舍去),
此时P点坐标为(1,
)、Q点坐标为(3,0),
设直线PQ的解析式为:y=kx+b,
则
,
解得
,
y=-
x+
;
若S△OPQ=
S△AOB,所列方程无解;
②当P在AB、Q在OB上,即2<t≤4时,S△PQB=-
t2+2
t,
当S△PQB=
S△AOB时,即=-
t2+2
t=
×4
,
解得t=3,
此时P为(3,
)、Q为(1,0),
设过点PQ的直线解析式为y=kx+b,即
,
解得
故直线PQ的解析式为:y=
x-
;
当S△PQB=
S△AOB时,即-
t2+2
t=
×4
时,此方程无解.
 解:(1)如图1,当P在OA上,即0≤t≤2时,过点P作PD⊥x轴,
解:(1)如图1,当P在OA上,即0≤t≤2时,过点P作PD⊥x轴,∵OP=2t,△AOB是等边三角形,
∴OD=OP•cos∠AOB=2t•
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴P(t,
| 3 |
当P在AB上,即2<t≤4时,过点P作PE⊥x轴,
∵OA+AB=8,
∴BP=8-2t,
∴BE=
| 8-2t |
| 2 |
| 3 |
| 3 |
∴P(t,4
| 3 |
| 3 |

∵OB=4,
∴OE=4-t,
∴Q(4-t,0),
故答案为:(t,
| 3 |
| 3 |
| 3 |
(2)如图2,当PQ⊥AO时,
∵∠AOB=60°,
∴∠OQP=30°,
∵OP=2t,OQ=4-t,
∴OQ=2OP,即4-t=2•2t,解得t=
| 4 |
| 5 |

如图3,当PQ⊥AB,
∵∠ABO=60°,
∴∠PQB=30°,
∵BP=8-2t,BQ=t,
∴BQ=2PB,即t=2(8-2t),解得t=
| 16 |
| 5 |
如图4,当PQ⊥OB,

由(1)得P点和Q点的横坐标总是相等的,
∴OQ=BQ,即4-t=t,解得t=2;
故答案为:
| 4 |
| 5 |
| 16 |
| 5 |
(3)①∵当0≤t≤2时,S=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
∴当t=-
2
| ||||
2•(-
|
0-(2
| ||||
4•(-
|
| 3 |
②当2<t≤4时,S=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
∴在2<t≤4范围内,S随t的增大而减小,并且当t=2时,S的最大值为2
| 3 |
∴2<t≤4时,S<2
| 3 |
综上所述,当t=2时,S有最大值2
| 3 |
(4)如图4,∵AQ=OAsin60°=4×
| ||
| 2 |
| 3 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
①当P在OA、Q在OB上,即0≤t≤2时,
∵S△OPQ=
| 3 |
| 8 |
∴-
| ||
| 2 |
| 3 |
3
| ||
| 2 |
解得t=1或3(舍去),
此时P点坐标为(1,
| 3 |
设直线PQ的解析式为:y=kx+b,
则
|
解得
|
y=-
| ||
| 2 |
3
| ||
| 2 |
若S△OPQ=
| 5 |
| 8 |
②当P在AB、Q在OB上,即2<t≤4时,S△PQB=-
| ||
| 2 |
| 3 |
当S△PQB=
| 3 |
| 8 |
| ||
| 2 |
| 3 |
| 3 |
| 8 |
| 3 |
解得t=3,
此时P为(3,
| 3 |
设过点PQ的直线解析式为y=kx+b,即
|
解得
|
故直线PQ的解析式为:y=
| ||
| 2 |
| ||
| 2 |
当S△PQB=
| 5 |
| 8 |
| ||
| 2 |
| 3 |
| 5 |
| 8 |
| 3 |
点评:本题考查的是相似形综合题,此题涉及到等边三角形的性质、三角形的面积公式、锐角三角函数的定义及用待定系数法求一次函数的解析式,涉及面较广,难度较大.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
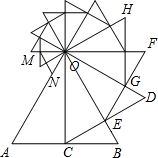 如图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时点N在OA上.若AB=1,则ON的长为( )
如图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时点N在OA上.若AB=1,则ON的长为( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
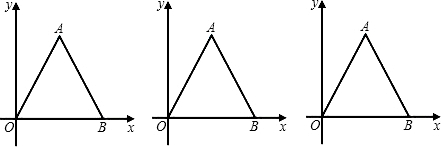
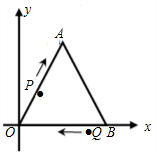 速度向终点B点运动,点Q从B点出发以1个单位/秒的速度向终点O点运动,两点同时出发,运动时间为t(单位:秒).
速度向终点B点运动,点Q从B点出发以1个单位/秒的速度向终点O点运动,两点同时出发,运动时间为t(单位:秒). 如图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最后得到△OMN,此时N在AO延长线上.若AB=1,则ON=
如图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最后得到△OMN,此时N在AO延长线上.若AB=1,则ON=