题目内容

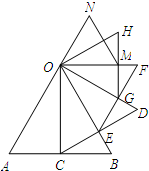如图，以等边△OAB的高OC为边向逆时针方向作等边△OCD，CD交OB于点E，再以OE为边向逆时针方向作等边△OEF，EF交OD于点G，再以OG为边向逆时针方向作等边△OGH，…，按此方法操作，最后得到△OMN，此时N在AO延长线上．若AB=1，则ON=
9
16
9
16
．
分析：先根据等边三角形的性质及锐角三角函数的定义分别求出OC、OE的长，找出规律即可得出ON的长．
解答：解：∵等边△ABC的边长为1，OC⊥AB，
∴OC=OA•sin60°=1×
3
2
=
3
2
，
同理，OE=OC•sin60°=
3
2
×
3
2
=（
3
2
）2=
3
4
，
OG=OE•sin60°=
3
4
×
3
2
=（
3
2
）3=
3
3
8
，
故OM=ON=（
3
2
）4=
9
16
．
故答案为：
9
16
．
点评：本题考查的是等边三角形的性质及锐角三角函数的定义，熟知锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
如图，以等边△OAB的边OB所在直线为x轴，点O为坐标原点，使点A在第一象限建立平面直角坐标系，其中△OAB边长为6个单位，点P从O点出发沿折线OAB向B点以3单位/秒的速度向B点运动，点Q从O点出发以2单位/秒的速度沿折线OBA向A点运动，两点同时出发，运动时间为t（单位：秒），当两点相遇时运动停止．
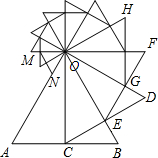精英家教网
（1）点A坐标为
 
，P、Q两点相遇时交点的坐标为
 
；
（2）当t=2时，S△OPQ=
 
；当t=3时，S△OPQ=
 
；
（3）设△OPQ的面积为S，试求S关于t的函数关系式；
（4）当△OPQ的面积最大时，试求在y轴上能否找一点M，使得以M、P、Q为顶点的三角形是Rt△？若能找到请求出M点的坐标，若不能找到请简单说明理由．
（原创题）如图，以等边△OAB的边OB所在直线为x轴，点O为坐标原点，使点A在第一象限建立平面直角坐标系，其中△OAB边长为4个单位，点P从O点出发沿折线OAB向B点以2个单位/秒的精英家教网速度向终点B点运动，点Q从B点出发以1个单位/秒的速度向终点O点运动，两点同时出发，运动时间为t（单位：秒）．
①直接写出P与Q点的坐标，并注明t的取值范围；
②当t=
 
时，PQ⊥OA；当t=
 
时，PQ⊥AB；当t=
 
时，PQ⊥OB；
③△OPQ面积为S，求S关于t的函数关系式并指出S的最大值；
④若直线PQ将△OAB分成面积比为3：5两部分，求此时直线PQ的解析式；若不能请说明理由．
精英家教网如图，以等边△OAB的高OC为边向逆时针方向作等边△OCD，CD交OB于点E，再以OE为边向逆时针方向作等边△OEF，EF交OD于点G，再以OG为边向逆时针方向作等边△OGH，…，按此方法操作，最终得到△OMN，此时点N在OA上．若AB=1，则ON的长为（　　）
A、(
3
2
)12
B、(
3
2
)10
C、(
3
3
)12
D、(
3
3
)10
如图，以等边△OAB的边OB所在直线为x轴，点O为坐标原点，使点A在第一象限建立平面直角坐标系，其中△OAB边长为4个单位，点P从O点出发沿折线OAB向B点以2个单位/秒的速度向终点B点运动，点Q从B点出发以1个单位/秒的速度向终点O点运动，两个点同时出发，运动时间为t（秒）．
（1）请用t表示点P的坐标
（t，
3
t）或（t，4
3
-
3
t）
（t，
3
t）或（t，4
3
-
3
t）
和点Q的坐标
（4-t，0）
（4-t，0）
，其中t的取值范围是
0≤t≤2或2＜t≤4
0≤t≤2或2＜t≤4
；
（2）当t=
4
5
4
5
时，PQ⊥OA；当t=
16
5
16
5
时，PQ⊥AB；当t=
2
2
时，PQ⊥OB；
（3）△OPQ面积为S，求S关于t的函数关系式并指出S的最大值；
（4）若直线PQ将△OAB分成面积比为3：5两部分？求此时直线PQ的解析式；若不能，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

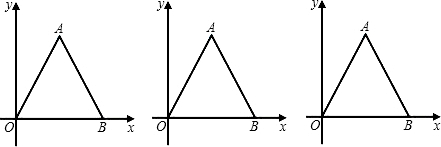
精英家教网