题目内容
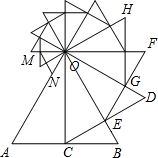 如图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时点N在OA上.若AB=1,则ON的长为( )
如图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时点N在OA上.若AB=1,则ON的长为( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
分析:利用正三角形的性质和正三角形的边长求得OC的长,然后逆时针旋转30°后可以求得OE的长,直至线段ON与线段OA重合,一共旋转了10次,从而可以求得ON的长.
解答:解:∵OC为等边三角形的高,且等边三角形的边长为1,
∴NC=
,
∵△OCD为等边三角形,
∴∠OCD=60°,
∴OE⊥CD,
∴OE=
×
=(
)2,
以此类推,当ON与OA重合时,一共旋转了10次,
∴ON的长为(
)10.
故选B.
∴NC=
| ||
| 2 |
∵△OCD为等边三角形,
∴∠OCD=60°,
∴OE⊥CD,
∴OE=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
以此类推,当ON与OA重合时,一共旋转了10次,
∴ON的长为(
| ||
| 2 |
故选B.
点评:本题考查了正三角形的性质,解题的关键是正确地得到一共旋转了多少次.

练习册系列答案
相关题目
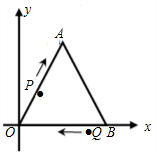 速度向终点B点运动,点Q从B点出发以1个单位/秒的速度向终点O点运动,两点同时出发,运动时间为t(单位:秒).
速度向终点B点运动,点Q从B点出发以1个单位/秒的速度向终点O点运动,两点同时出发,运动时间为t(单位:秒).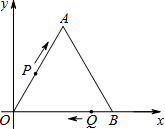 终点O点运动,两个点同时出发,运动时间为t(秒).
终点O点运动,两个点同时出发,运动时间为t(秒). 如图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最后得到△OMN,此时N在AO延长线上.若AB=1,则ON=
如图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最后得到△OMN,此时N在AO延长线上.若AB=1,则ON=