题目内容
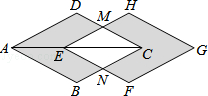
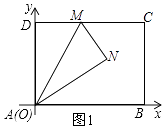
【题目】如图，在边长为a（a＞2）的正方形各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠CHN=∠DEP=45°时，则正方形MNPQ的面积为 ．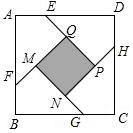 
【答案】2
【解析】解：分别延长QE，MF，NG，PH，交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形（如图（2））．若将上述四个等腰三角形拼成一个新的正方形（无缝隙，不重叠），则新正方形的边长a；这个新正方形与原正方形ABCD的面积相等； 通过上述的分析，可以发现S正方形MNPQ=4S△FSB=4 
×1×1=2．
所以答案是2．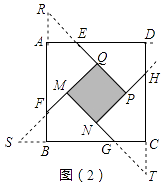
【考点精析】利用正方形的性质对题目进行判断即可得到答案，需要熟知正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
相关题目
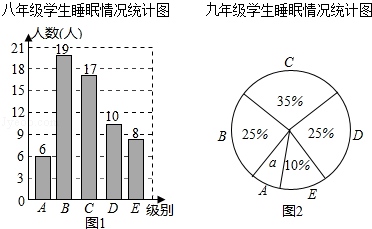
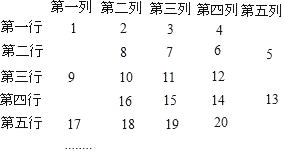
【题目】为了解某校八、九年级部分学生的睡眠情况，随机抽取了该校八、九年级部分学生进行调查，已知抽取的八年级与九年级的学生人数相同，利用抽样所得的数据绘制如图的统计图表：
睡眠情况分段情况如下
组别 | 睡眠时间x（小时） |
A | 4.5≤x＜5.5 |
B | 5.5≤x＜6.5 |
C | 6.5≤x＜7.5 |
D | 7.5≤x＜8.5 |
E | 8.5≤x＜9.5 |
根据图表提供的信息，回答下列问题：
（Ⅰ）直接写出统计图中a的值 
（Ⅱ）睡眠时间少于6.5小时为严重睡眠不足，则从该校八、九年级各随机抽一名学生，被抽到的这两位学生睡眠严重不足的可能性分别有多大？
