题目内容
【题目】如图,在平面直角坐标系中有一个四边形OABC,其中CB∥x轴,OC=3,BC=2,∠OAB=45°. 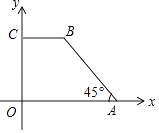
(1)求点A,B的坐标;
(2)求出直线AB的解析式.
【答案】
(1)解:如图,过B作BD⊥OA于D,则四边形ODBC是矩形,
∴OD=BC=2,BD=OC=3,
∵∠OAB=45°,
∴AD=BD=3,
∴OA=5,
∴A(5,0),B(2,3)

(2)解:设直线AB的解析式为y=kx+b,
则 ![]() ,解得
,解得 ![]() ,
,
所以直线AB的解析式为y=﹣x+5
【解析】(1)过B作BD⊥OA于D,则四边形ODBC是矩形,OD=BC=2,BD=OC=3,再根据∠OAB=45°,得出AD=BD=3,那么OA=5,进而求出A,B的坐标.(2)利用待定系数法将A,B的坐标代入即可求解.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目