题目内容
【题目】如图，一次函数y=ax﹣b与正比例函数y=kx的图象交于第三象限内的点A，与y轴交于B（0，﹣4），且OA=AB，△AOB的面积为6．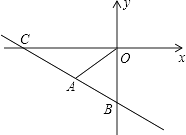
（1）求两个函数的解析式；
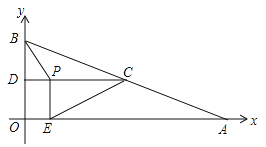
（2）若有一个点M（2，0），直线BM与AO交于点P，求点P的坐标；
（3）在x轴上是否存在点E，使S△ABE=5？若存在，求点E的坐标；若不存在，请说明理由．
【答案】
（1）
解：如图1，
作AD⊥OB轴于D，
∵B（0，﹣4），
∴OB=4，
∵OA=AB，
∴OD=BD= 
OB=2，
∵S△AOB=6，
∴S△AOB= OBAD= ×4AD=6，
∴AD=3
而点A在第三象限内，则A（﹣3，﹣2），
又点A在y=kx上，
∴﹣2=﹣3k，∴k= 
，
∴正比例函数解析式为：y= x，
又y=ax﹣b通过A、B，
∴ 
，
∴ 
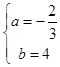
∴一次函数解析式为：y=﹣ x﹣4
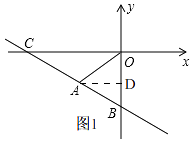
（2）
解：由（1）知，正比例函数解析式为：y= x①，
∵B（0，﹣4），M（2，0），
∴直线BM的解析式为y=2x﹣4②，
联立①②得，点P（3，2）
（3）
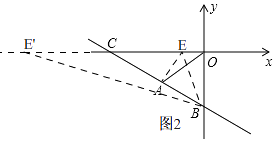
解：如图2，
由（1）知，一次函数解析式为：y=﹣ x﹣4
∴C（﹣6，0）
∵点E在x轴上，设E（x，0），
∴CE=|x+6|，
∵S△ABE=5，
S△ABE=S△BCE﹣S△ACE= BE|yB|﹣ BE|yA|= BE（|yB|﹣|yA|）= |x+6|（4﹣2）=|x+6|=5
∴x=﹣1或x=﹣11；
∴E（﹣1，0）或（﹣11，0）能够使得△ABE的面积为5．
【解析】（1）利用等腰三角形的三线合一得出OD= OB=2，再用三角形的面积求出AD=3，即可得出结论；（2）利用待定系数法求出直线BM的解析式和正比例函数解析式，联立即可得出结论；（3）利用三角形的面积的差，建立方程求解即可得出结论．
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识，掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小．
