题目内容
一个等腰三角形的一边长为4,另两边长是关于x的方程x2+2mx+1-2m=0的两根,求此三角形的周长.
解:∵一个等腰三角形的一边长为4,另两边长是关于x的方程x2+2mx+1-2m=0的两根,
①当腰长为4时,把x=4代入原方程得
16+8m+1-2m=0,
∴m=-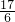 ,
,
∴原方程变为:x2- x+
x+ =0,
=0,
设方程的另一个根为x,
则4+x= ,
,
∴x= ,
,
∴三角形的周长为:4+4+ =
= ;
;
②当底边为4时,那么x的方程x2+2mx+1-2m=0的两根是相等的,
∴△=(2m)2-4(1-2m)=0,
∴m=-1+ 或m=-1-
或m=-1- ,
,
但是m=-1- 时方程的根为负数,而方程的根是线段长度,不能为负,
时方程的根为负数,而方程的根是线段长度,不能为负,
∴m=-1+ ,
,
∴方程变为x2+2(-1- )x+1-2(-1+
)x+1-2(-1+ )=0,
)=0,
∴方程的两根相等为x1=x2= +1,
+1,
∴三角形的周长为4+2( +1)=6+2
+1)=6+2 .
.
分析:由于一个等腰三角形的一边长为4,另两边长是关于x的方程x2+2mx+1-2m=0的两根,有两种情况:
①当腰长为4时,直接把x=4代入原方程即可求出m的值,然后求出方程的另一根,也就可以求出三角形的周长;
②当底边为4时,那么x的方程x2+2mx+1-2m=0的两根是相等的,利用判别式为0即可求出m的值,然后就可以求出方程的解,也就可以求出三角形的周长.
点评:此题主要考查了一元二次方程的解的定义和等腰三角形的性质,解题的关键是利用等腰三角形的性质得到方程的解,把方程的解代入原方程即可求出待定字母的取值即可解决问题.
①当腰长为4时,把x=4代入原方程得
16+8m+1-2m=0,
∴m=-
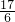 ,
,∴原方程变为:x2-
 x+
x+ =0,
=0,设方程的另一个根为x,
则4+x=
 ,
,∴x=
 ,
,∴三角形的周长为:4+4+
 =
= ;
;②当底边为4时,那么x的方程x2+2mx+1-2m=0的两根是相等的,
∴△=(2m)2-4(1-2m)=0,
∴m=-1+
 或m=-1-
或m=-1- ,
,但是m=-1-
 时方程的根为负数,而方程的根是线段长度,不能为负,
时方程的根为负数,而方程的根是线段长度,不能为负,∴m=-1+
 ,
,∴方程变为x2+2(-1-
 )x+1-2(-1+
)x+1-2(-1+ )=0,
)=0,∴方程的两根相等为x1=x2=
 +1,
+1,∴三角形的周长为4+2(
 +1)=6+2
+1)=6+2 .
.分析:由于一个等腰三角形的一边长为4,另两边长是关于x的方程x2+2mx+1-2m=0的两根,有两种情况:
①当腰长为4时,直接把x=4代入原方程即可求出m的值,然后求出方程的另一根,也就可以求出三角形的周长;
②当底边为4时,那么x的方程x2+2mx+1-2m=0的两根是相等的,利用判别式为0即可求出m的值,然后就可以求出方程的解,也就可以求出三角形的周长.
点评:此题主要考查了一元二次方程的解的定义和等腰三角形的性质,解题的关键是利用等腰三角形的性质得到方程的解,把方程的解代入原方程即可求出待定字母的取值即可解决问题.

练习册系列答案
相关题目