ĚâÄżÄÚČÝ
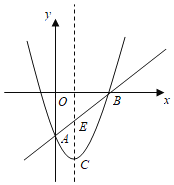
ˇľĚâÄżˇżŇŃÖŞĹ×Îďy=ax2+bx+c(b<0)ÓëÖáÖ»ÓĐŇ»¸öą«ą˛µă.
(1)Čôą«ą˛µă×ř±ęÎŞ(2Ł¬0)Ł¬Çóaˇ˘cÂú×ăµÄąŘϵʽŁ»
(2)ÉčAÎŞĹ×ÎďĎßÉϵÄŇ»¶¨µăŁ¬Ö±ĎßlŁşy=kx+1ŁkÓëĹ×ÎďĎß˝»ÓÚµăBˇ˘CÁ˝µăŁ¬Ö±ĎßBD´ąÖ±ÓÚÖ±Ďßy=Ł1,´ą×ăÎŞµăD.µ±kŁ˝0ʱŁ¬Ö±ĎßlÓëĹ×ÎďĎßµÄŇ»¸ö˝»µăÔÚyÖáÉĎŁ¬Çҡ÷ABCÎŞµČŃüÖ±˝ÇČý˝ÇĐÎ.
˘ŮÇóµăAµÄ×ř±ęşÍĹ×ÎďĎߵĽâÎöĘ˝Ł»
˘ÚÖ¤Ă÷Łş¶ÔÓÚĂż¸ö¸ř¶¨µÄʵĘýkŁ¬¶ĽÓĐAˇ˘Dˇ˘CČýµăą˛Ďß.
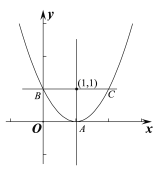
ˇľ´đ°¸ˇż(1) y=a(xŁ2)2, c=4a;(2) ˘Ů¶ĄµăA(1,0)Ł¬y= x2Ł2x+1,˘ÚĽű˝âÎö.
ˇľ˝âÎöˇż
Ł¨1Ł©¸ůľÝĹ×ÎďĎßÓëxÖáµÄą«ą˛µă×ř±ęĽ´ÎŞşŻĘý¶Ąµă×ř±ęŁ¬Ľ´żÉÇó˝âŁ»
Ł¨2Ł©˘ŮyŁ˝kxŁ«1kŁ˝kŁ¨x1Ł©Ł«1ąý¶¨µăŁ¨1Ł¬1Ł©Ł¬Çҵ±kŁ˝0ʱŁ¬Ö±Ďßl±äÎŞyŁ˝1Ć˝ĐĐxÖᣬÓëÖáµÄ˝»µăÎŞŁ¨0Ł¬1Ł©Ł¬Ľ´żÉÇó˝âŁ»˘ÚĽĆËăÖ±ĎßAD±í´ďĘ˝ÖеÄkÖµˇ˘Ö±ĎßAC±í´ďĘ˝ÖеÄkÖµŁ¬Á˝¸ökÖµĎŕµČĽ´żÉÇó˝âŁ®
˝âŁşŁ¨1Ł©Ĺ×ÎďĎßÓëxÖáµÄą«ą˛µă×ř±ęĽ´ÎŞşŻĘý¶Ąµă×ř±ęŁ¬ąĘŁşyŁ˝aŁ¨x2Ł©2Ł¬ÔňcŁ˝4aŁ»
(2) y=kx+1Łk= k(xŁ1)+1ąý¶¨µă(1,1),
Çҵ±kŁ˝0ʱŁ¬Ö±Ďßl±äÎŞy=1Ć˝ĐĐxÖá,ÓëyÖáµÄ˝»µăÎŞ(0,1)
ÓÖˇ÷ABCÎŞµČŃüÖ±˝ÇČý˝ÇĐÎŁ¬ˇŕµăAÎŞĹ×ÎďĎߵĶĄµă
˘Ůc=1Ł¬¶ĄµăA(1,0)
Ĺ×ÎďĎߵĽâÎöĘ˝: y= x2Ł2x+1.
˘Ú![]()
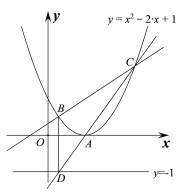
x2Ł(2+k)x+kŁ˝0,
xŁ˝![]() (2+kˇŔ
(2+kˇŔ![]() )
)
xDŁ˝xBŁ˝![]() (2+kŁ
(2+kŁ![]() ), yD=Ł1Ł»
), yD=Ł1Ł»
ÔňD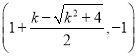
yCŁ˝![]() (2+k2+k
(2+k2+k![]() ,
,
C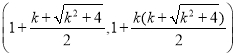 Ł¬A(1,0)
Ł¬A(1,0)
ˇŕÖ±ĎßAD±í´ďĘ˝ÖеÄkֵΪŁşk AD=![]() =
=![]() Ł¬
Ł¬
Ö±ĎßAC±í´ďĘ˝ÖеÄkֵΪŁşk AC=![]()
ˇŕk AD= k AC, µăAˇ˘Cˇ˘DČýµăą˛Ďß.