题目内容
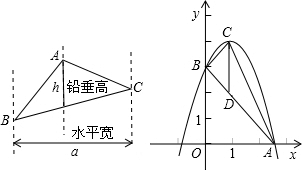
阅读材料:如图,过△ABC的三个顶点分别作出水平垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可以得出一种计算三角形面积的新方法:S△ABC= ah,即三角形面积等于水平宽与铅垂高乘积的一半.
ah,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:如图,抛物线顶点坐标为点C(1,4)交x轴于点A,交y轴于点B(0,3)

(1)求抛物线解析式和线段AB的长度;
(2)点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
(3)在第一象限内求一点P,使S△PAB=S△CAB.
解:(1)设抛物线的解析式为: ,
,
把B(0,3)代入解析式求得a=-1
所以 ,
,
令y1=0,得0=-x2+2x+3,解得x1=-1,x2=3
∴A点的坐标为(3,0)
∴AB=3 ;
;
(2)设直线AB的解析式为:y2=kx+b
由A(3,0),B(0,3)
∴
∴直线AB的解析式为y2=-x+3 …
因为C点坐标为(1,4),
所以当x=1时,y1=4,y2=2,
所以CD=4-2=2,
 (平方单位);
(平方单位);
(3)设P点的横坐标为x,△PAB的铅垂高为h,
则 ;
;
由S△PAB=S△CAB得:
 ,
,
解得x=2或x=1(舍).
所以P(2,3).
分析:(1)利用顶点式求得抛物线的解析式,然后求得点A的坐标,从而求得线段AB的长;
(2)利用待定系数法求得直线AB的解析式,然后求得CD的长,从而求得三角形ABC的面积;
(3)设P点的横坐标为x,△PAB的铅垂高为h,表示出h关于x的函数关系式,然后利用面积相等求得x的值,从而确定点P的坐标.
点评:此题主要考查了用顶点式求二次函数解析式,以及待定系数法求解析式和三角形面积求法,综合性较强.
 ,
,把B(0,3)代入解析式求得a=-1
所以
 ,
,令y1=0,得0=-x2+2x+3,解得x1=-1,x2=3
∴A点的坐标为(3,0)
∴AB=3
 ;
;(2)设直线AB的解析式为:y2=kx+b
由A(3,0),B(0,3)
∴

∴直线AB的解析式为y2=-x+3 …
因为C点坐标为(1,4),
所以当x=1时,y1=4,y2=2,
所以CD=4-2=2,
 (平方单位);
(平方单位);(3)设P点的横坐标为x,△PAB的铅垂高为h,
则
 ;
;由S△PAB=S△CAB得:
 ,
,解得x=2或x=1(舍).
所以P(2,3).
分析:(1)利用顶点式求得抛物线的解析式,然后求得点A的坐标,从而求得线段AB的长;
(2)利用待定系数法求得直线AB的解析式,然后求得CD的长,从而求得三角形ABC的面积;
(3)设P点的横坐标为x,△PAB的铅垂高为h,表示出h关于x的函数关系式,然后利用面积相等求得x的值,从而确定点P的坐标.
点评:此题主要考查了用顶点式求二次函数解析式,以及待定系数法求解析式和三角形面积求法,综合性较强.

练习册系列答案
相关题目


 阅读材料:
阅读材料:
 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
 S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.