题目内容
 阅读材料:
阅读材料:如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.
我们可得出一种计算三角形面积的新方法:S△ABC=
| 1 | 2 |
解答下列问题:
已知:直线l1:y=-2x+6与x轴交于点A,直线l2:y=x+3与y轴交于点B,直线l1、l2交于点C.
(1)建立平面直角坐标系,画出示意图(无需列表)并求出C点的坐标;
(2)利用阅读材料提供的方法求△ABC的面积.
分析:(1)联立两解析式,可求出点C的坐标;
(2)先画出图形,然后根据阅读材料所提供的信息,求出“水平宽”、“铅垂高”,然后计算即可.
(2)先画出图形,然后根据阅读材料所提供的信息,求出“水平宽”、“铅垂高”,然后计算即可.
解答:解:(1)

联立两解析式:
,
解得:
,
故点C的坐标为(1,4).
(2)
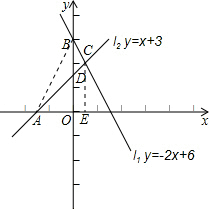
如图所示:点A的坐标为(-3,0),点B的坐标为(0,6),
水平宽AE=4,铅直高BD=3,
∴S△ABC=
AE×BD=6.

联立两解析式:
|
解得:
|
故点C的坐标为(1,4).
(2)
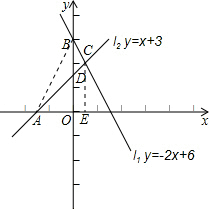
如图所示:点A的坐标为(-3,0),点B的坐标为(0,6),
水平宽AE=4,铅直高BD=3,
∴S△ABC=
| 1 |
| 2 |
点评:本题考查了一次函数的综合,阅读材料获取解题信息是解题关键,立意新颖,难度适中,是难得的好题目.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目


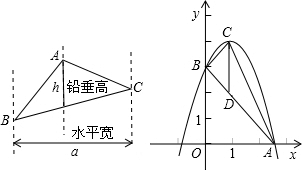
 ah,即三角形面积等于水平宽与铅垂高乘积的一半.
ah,即三角形面积等于水平宽与铅垂高乘积的一半.
 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
 S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.