题目内容
 29、如图,Rt△ABC内接于⊙O,∠A=30°,延长斜边AB到D,使BD等于⊙O半径,求证:DC是⊙O切线.
29、如图,Rt△ABC内接于⊙O,∠A=30°,延长斜边AB到D,使BD等于⊙O半径,求证:DC是⊙O切线.分析:连OC,由∠A=30°,可得∠COB=60°,由此判断△COB为等边三角形,得到BC=BO,再由BD等于⊙O半径,得到BC=BO=BD,因此可判断△OCD为直角三角形,即∠OCB=90°.
解答:证明:连OC,如图,
∵∠A=30°,OA=OC,
∴∠COB=60°,
∵△COB为等边三角形,
∴BC=BO,
而BD等于⊙O半径,
∴BC=BO=BD,
∴△OCD为直角三角形,即∠OCB=90°,
所以DC是⊙O切线.

∵∠A=30°,OA=OC,
∴∠COB=60°,
∵△COB为等边三角形,
∴BC=BO,
而BD等于⊙O半径,
∴BC=BO=BD,
∴△OCD为直角三角形,即∠OCB=90°,
所以DC是⊙O切线.
点评:本题考查了圆的切线的判定方法.若直线与圆有唯一的公共点,则此直线是圆的切线;若圆心到直线的距离等于圆的半径,则此直线是圆的切线;经过半径的外端点与半径垂直的直线是圆的切线.当已知直线过圆上一点,要证明它是圆的切线,则要连接圆心和这个点,证明这个连线与已知直线垂直即可;当没告诉直线过圆上一点,要证明它是圆的切线,则要过圆心作直线的垂线,证明垂线段等于圆的半径.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
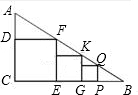 如图,Rt△ABC内有三个内接正方形,DF=18,GK=12,则PQ=
如图,Rt△ABC内有三个内接正方形,DF=18,GK=12,则PQ=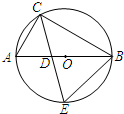 如图,Rt△ABC内接于⊙O,∠ACB的平分线分别交AB、⊙O于点D、E.
如图,Rt△ABC内接于⊙O,∠ACB的平分线分别交AB、⊙O于点D、E.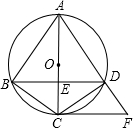 如图,Rt△ABC内接于⊙O.将⊙O沿直径AC对折,B点落在圆上D点处.连接BD交AC于点E,过C点作BD的平行线交AD的延长线于点F.
如图,Rt△ABC内接于⊙O.将⊙O沿直径AC对折,B点落在圆上D点处.连接BD交AC于点E,过C点作BD的平行线交AD的延长线于点F. (2013•南通)如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是
(2013•南通)如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是