题目内容
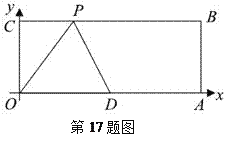
【题目】如图,抛物线y=﹣x2+4与x轴交于A、B两点,与y轴交于C点,点P是抛物线上的一个动点且在第一象限,过点P作x轴的垂线,垂足为D,交直线BC于点E.
(1)求点A、B、C的坐标和直线BC的解析式;
(2)求△ODE面积的最大值及相应的点E的坐标;
(3)是否存在以点P、O、D为顶点的三角形与△OAC相似?若存在,请求出点P的坐标,若不存在,请说明理由.

【答案】(1)A(﹣2,0)、B(2,0)、C(0,4),y=﹣2x+4.(2)△ODE的面积有最大值1.点E的坐标为(1,2).(3)(![]() -1,2
-1,2![]() -2),(
-2),(![]() ,
, ![]() ).
).
【解析】试题分析:(1)在抛物线解析式y=﹣x2+4中,令y=0,解方程可求得点A、点B的坐标;令x=0,可求得顶点C的坐标.已知点B、C的坐标,利用待定系数法求出直线BC的解析式。
(2)求出△ODE面积的表达式,利用二次函数的性质求出最大值,并确定点E的坐标。
(3)本问为存在型问题.因为△OAC与△OPD都是直角三角形,需要分类讨论:
①当△PDO∽△COA时,由![]() 得PD=2OD,列方程求出点P的坐标;
得PD=2OD,列方程求出点P的坐标;
②当△PDO∽△AOC时,由![]() 得OD=2PD,列方程求出点P的坐标。
得OD=2PD,列方程求出点P的坐标。
解:(1)在y=﹣x2+4中,当y=0时,即﹣x2+4=0,解得x=±2;
当x=0时,即y=0+4,解得y=4。
∴点A、B、C的坐标分别为A(﹣2,0)、B(2,0)、C(0,4)。
设直线BC的解析式为y=kx+b(k≠0),
则![]() ,解得
,解得![]() 。
。
∴直线BC的解析式为y=﹣2x+4。
(2)∵点E在直线BC上,∴设点E的坐标为(x,﹣2x+4)。
∴△ODE的面积S可表示为:![]() 。
。
∴当x=1时,△ODE的面积有最大值1。
此时,﹣2x+4=﹣2×1+4=2,∴点E的坐标为(1,2)。
(3)存在以点P、O、D为顶点的三角形与△OAC相似。理由如下:
设点P的坐标为(x,﹣x2+4),0<x<2.
因为△OAC与△OPD都是直角三角形,分两种情况:
①当△PDO∽△COA时,![]() ,即
,即![]() ,
,
解得![]() (不符合题意,舍去)。
(不符合题意,舍去)。
当![]() 时,
时,![]() 。
。
∴此时,点P的坐标为![]() 。
。
②当△PDO∽△AOC时,![]() ,
,![]() ,
,
解得![]() (不符合题意,舍去)。
(不符合题意,舍去)。
当![]() 时,
时,![]() 。
。
∴此时,点P的坐标为![]() 。
。
综上所述,满足条件的点P有两个:P1![]() ,P2
,P2![]() 。
。