题目内容
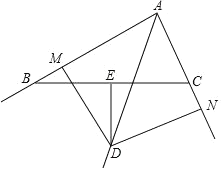
【题目】如图,点P是正方形ABCD内的一点,且PA=1,PB=PD=![]() ,则∠APB的度数为_______.
,则∠APB的度数为_______.

【答案】105°
【解析】
过点P作PH⊥AB于H,由全等可知∠BAP=∠DAP=45°,从而得到∠APH=45°,然后通过AP可求出HP的长,从而得到∠BPH,即可得到∠APB的度数.
解:过点P作PH⊥AB于H,

∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
在△APB和△APD中
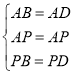
∴△APB≌△APD,
∴∠BAP=∠DAP,
由∠BAD=90°,可知∠BAP=∠DAP=45°,
∴∠APH=90°-45°=45°,
∵PA=1,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵PB=![]() ,
,
∴∠PBA=30°,
∴∠BPH=90°-30°=60°,
∴∠APB=∠APH+∠BPH=45°+60°=105°

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目