题目内容
如图，在平行四边形ABCD中，CE＝AF，求证：四边形BEDF是平行四边形。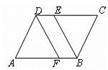
证明：在平行四边形ABCD中
AB∥DC，AB＝DC
又CE＝AF
∴DE＝BF
而DE∥BF
∴四边形BEDF是平行四边形
AB∥DC，AB＝DC
又CE＝AF
∴DE＝BF
而DE∥BF
∴四边形BEDF是平行四边形
由平行四边形的性质可得：AB与CD平行且相等；而CE＝AF，可得DE与BF平行且相等，由此可证得四边形BEDF是平行四边形．
练习册系列答案
相关题目
题目内容
于E，
于F。猜想DE、EF、FB之间的数量关系，并对你的猜想加以证明。
< S△OQB，若存在，求出t的取值范围，若不存在，试说明理由。 