题目内容
已知一个等腰三角形的腰长是a,底角是15度.则此等腰三角形的面积为分析:由已知条件,根据等腰三角形的性质和三角形内外角关系解答,得到30°的角,利用直角三角形的性质可得答案.
解答: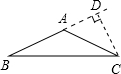 解:如图,延长BA,作CD⊥AB于D,
解:如图,延长BA,作CD⊥AB于D,
∵△ABC是等腰三角形,
∴∠DAC=2∠ABC=2×15°=30°,
∵CD⊥AB,
∴CD=
AC=0.5a,
等腰三角形的面积为:
×a×0.5a=
a2.
故填
a2.
 解:如图,延长BA,作CD⊥AB于D,
解:如图,延长BA,作CD⊥AB于D,∵△ABC是等腰三角形,
∴∠DAC=2∠ABC=2×15°=30°,
∵CD⊥AB,
∴CD=
| 1 |
| 2 |
等腰三角形的面积为:
| 1 |
| 2 |
| 1 |
| 4 |
故填
| 1 |
| 4 |
点评:本题考查了等腰三角形的性质、三角形外角的性质及含30°角的直角三角形的性质;解答此题的关键是作出辅助线,构造特殊角,然后根据特殊三角形的性质解答.

练习册系列答案
相关题目
已知一个等腰三角形的底边长为5,这个等腰三角形的腰长为x,则x的取值范围是( )
A、0<x<
| ||
B、x≥
| ||
C、x>
| ||
| D、0<x<10 |