题目内容
 21、已知:如图,在正方形ABCD中,点E是BC边的中点,连接AE并延长交CD的延长线与点G.
21、已知:如图,在正方形ABCD中,点E是BC边的中点,连接AE并延长交CD的延长线与点G.(1)写出图中的一对全等三角形,并证明;
(2)在正方形的边CD上用尺规作图的方法找一点F,使得AE平分∠BAF.(保留作图痕迹)
分析:因为∠GCE=∠B=90°,CE=BE,∠CEG=∠BEA,所以利用ASA判定△AEB≌△GEC.
作线段AG的中垂线交DC于点F,则AE平分∠BAF.
作线段AG的中垂线交DC于点F,则AE平分∠BAF.
解答: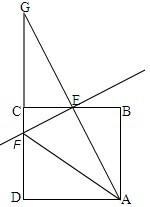 解:(1)△AEB≌△GEC.
解:(1)△AEB≌△GEC.
∵在正方形ABCD中,点E是BC边的中点,
∴∠GCE=∠B=90°,CE=BE.
∵∠CEG=∠BEA,
∴△AEB≌△GEC(ASA).(4分)
(2)作线段AG的中垂线交DC于点F,(8分)
∵△AEB≌△GEC,
∴∠G=∠EAB.
∵GE=AE,∠GEF=∠FEF=90°,EF=EF,
∴△GEF≌△AEF.
∴∠G=∠EAF.
∴∠EAF=∠EAB.
即AE平分∠BAF.
 解:(1)△AEB≌△GEC.
解:(1)△AEB≌△GEC.∵在正方形ABCD中,点E是BC边的中点,
∴∠GCE=∠B=90°,CE=BE.
∵∠CEG=∠BEA,
∴△AEB≌△GEC(ASA).(4分)
(2)作线段AG的中垂线交DC于点F,(8分)
∵△AEB≌△GEC,
∴∠G=∠EAB.
∵GE=AE,∠GEF=∠FEF=90°,EF=EF,
∴△GEF≌△AEF.
∴∠G=∠EAF.
∴∠EAF=∠EAB.
即AE平分∠BAF.
点评:此题考查基本的作图法及全等三角形的判定方法,常用的判定方法有SSS,SAS,AAS,HL(直角三角形)等,做题时要灵活运用.

练习册系列答案
相关题目
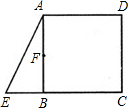 已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=
已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=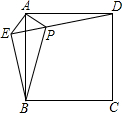 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=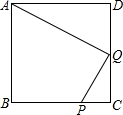 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?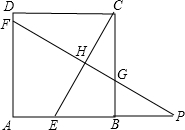 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.
已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.