Question

已知：如图，在正方形ABCD中，AB=8，点E在边AB上点，CE的垂直平分线FP 分别交AD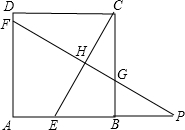、CE、CB于点F、H、G，交AB的延长线于点P．
（1）求证：△EBC∽△EHP；
（2）设BE=x，BP=y，求y与x之间的函数解析式，并写出定义域；
（3）当BG=

7

4

时，求BP的长．

Answer 1

分析：（1）由于在正方形ABCD中，∠ABC=90°，PH⊥CE，由此得到∠PHE=∠CBE=90°，又∠BEC=∠HEP，由此即可证明△EBC∽△EHP；
（2）在Rt△BCE中，根据勾股定理得到CE²=BE²+BC²=x²+64，根据（1）得到

BE

EH

=

CE

EP

，而EH=

1

2

CE，进一步得到

1

2

CE2=BE•EP，由此即可得到等式

1

2

(x2+64)=x(x+y)，变形后即可得到函数解析式，结合已知条件可以确定定义域；
（3）根据（1）知道∠ECB=∠P，而∠EBC=∠GBP=90°，由此可以证明△EBC∽△GBP，接着利用相似三角形的性质得到 GB•BC=BE•BP，接着得到

7

4

×8=x•

64-x2

2x

，解方程即可求解．

解答：（1）证明：∵在正方形ABCD中，∠ABC=90°，PH⊥CE，
∴∠PHE=∠CBE=90°（1分）
又∵∠BEC=∠HEP，
∴△EBC∽△EHP；

（2）解：在Rt△BCE中，CE²=BE²+BC²=x²+64．（1分）
∵△EBC∽△EHP，
∴

BE

EH

=

CE

EP

．（1分）
∴BE•EP=EH•EC．
∵EH=

1

2

CE．
∴

1

2

CE2=BE•EP．（1分）
∴

1

2

(x2+64)=x(x+y)，（1分）
∴函数解析式为y=

64-x2

2x

，（1分）
定义域为0＜x＜8．（1分）

（3）解：∵△EBC∽△EHP，
∴∠ECB=∠P，
∵∠EBC=∠GBP=90°．
∴△EBC∽△GBP．（1分）
∴

GB

BE

=

BP

BC

．（1分）
∴GB•BC=BE•BP．
∴

7

4

×8=x•

64-x2

2x

（1分）
∴x=±6（负值不符合题意，舍去），
∴BP=

7

3

．（1分）

点评：此题分别考查了相似三角形的性质与判定、正方形的性质及勾股定理，有一定的综合性，解题时要求学生分析问题、解决问题的能力比较强才能很好解决这类问题．