题目内容
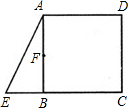 已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=
已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=| 1 | 2 |
解:连接
分析:连接CF,则CF=AE(也可连接FD),根据正方形的性质可知AB=CB,∠ABE=∠CBF,EB=FB,所以△ABE≌△CBF,则AE=CF.
解答: 解:连接CF,则CF=AE(也可连接FD),
解:连接CF,则CF=AE(也可连接FD),
∵正方形ABCD,
∴AB=BC,∠ABC=∠ABE=90°,
因为F是AB的中点,
∴FB=
AB,
∵EB=
BC,
∴EB=FB,
在△ABE和△CBF中,
.
∴△ABE≌△CBF,
∴AE=CF.
 解:连接CF,则CF=AE(也可连接FD),
解:连接CF,则CF=AE(也可连接FD),∵正方形ABCD,
∴AB=BC,∠ABC=∠ABE=90°,
因为F是AB的中点,
∴FB=
| 1 |
| 2 |
∵EB=
| 1 |
| 2 |
∴EB=FB,
在△ABE和△CBF中,
|
∴△ABE≌△CBF,
∴AE=CF.
点评:主要考查了正方形的性质和三角形全等的性质及判定.注意正方形是特殊条件最多的特殊平行四边形.要掌握才会灵活运用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
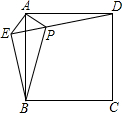 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=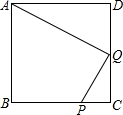 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?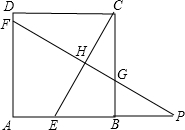 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.
已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.