题目内容
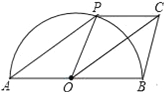
【题目】如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的动点,BC∥OP,BC=OP.
(1)求证:四边形AOCP是平行四边形;
(2)若AB=4,填空:
①当AP= 时,四边形AOCP是菱形;
②当AP= 时,四边形OBCP是正方形.
【答案】(1)证明见解析(2)①2;②2![]()
【解析】试题分析:(1)根据一组对边平行且相等的四边形是平行四边形,得到平行四边形OBCP,然后再根据平行四边形的性质和圆的半径,得到OA=PC,最后根据一组对边平行且相等的四边形是平行四边形,证明即可;
(2)①根据一组领边相等的平行四边形是菱形可求得结果;
②根据对角线互相垂直且相等的平行四边形是正方形,可证明.
试题解析:(1)∵BC∥OP,BC=OP,∴四边形OBCP是平行四边形,∴OB=PC,OB∥PC,
∵AB是半圆O的直径,∴OA=OB,∴OA=PC,
∵OB∥PC,∴四边形AOCP是平行四边形
(2)①2;②2![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目