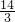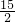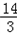题目内容
若a、b满足3a2+5|b|=7，S=2a2-3|b|，则S的最大值是（ ）
分析：先根据3a2+5|b|=7求出|b|的值，再代入S=2a2-3|b|中即可得到关于a的二次函数，根据a2的取值范围，二次函数的图象，求出S的最大值即可．
解答：解：由3a2+5|b|=7得|b|=
，
则
≥0，解得a2≤
，
将|b|=
代入S=2a2-3|b|中，
得S=
a2-
，
∵0≤a2≤
，S是关于a的二次函数，开口向上，
∴当a2=
时，S取最大值为S=
×
-
=
，
故选B．
| 7-3a2 |
| 5 |
则
| 7-3a2 |
| 5 |
| 7 |
| 3 |
将|b|=
| 7-3a2 |
| 5 |
得S=
| 19 |
| 5 |
| 21 |
| 5 |
∵0≤a2≤
| 7 |
| 3 |
∴当a2=
| 7 |
| 3 |
| 19 |
| 5 |
| 7 |
| 3 |
| 21 |
| 5 |
| 14 |
| 3 |
故选B．
点评：本题考查了非负数的性质及绝对值的性质．关键是根据已知等式“消元”，转化为二次函数，根据绝对值，偶次方根的性质求自变量的取值范围．
练习册系列答案
阅读快车系列答案
相关题目
